题目内容
12.若(x+y)3(2x-y+a)5的展开式中各项系数的和为256,则该展开式中含字母x且x的次数为1的项的系数为0.分析 二项式(x+y)3(2x-y+a)5中,令x=y=1得展开式各项系数和,求出a的值;
再求(x+y)3(2x-y+1)5的展开式中含字母x且x的系数.
解答 解:(x+y)3(2x-y+a)5的展开式中各项系数的和为256,
令 x=y=1,得23×(a+1)5=256,
解得a=1,
所以(x+y)3(2x-y+1)5的展开式中:
(x+y)3=x3+3x2y+3xy2+y3,
(2x-y+1)5=[2x+(1-y)]5
=32x5+${C}_{5}^{1}$•24•x4•(1-y)+…+${C}_{5}^{4}$•2x•(1-y)4+(1-y)5,
所以(x+y)3(2x-y+1)5的展开式中含字母x项为:
3xy•(1-y)5+y3•${C}_{5}^{4}$•2x•(1-y)4,
令y=1求得含x项的系数为0+0=0.
故答案为:0.
点评 本题考查了二项式定理与两个计数原理的应用问题,是易错题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
17.某棱锥的三视图如图所示,则该棱锥的外接球的表面积为( )
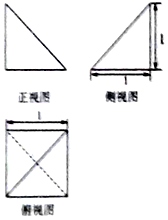

| A. | 3π | B. | 2π | C. | π | D. | 4π |
1.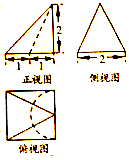 某零件的三视图如图所示,则该零件的体积为( )
某零件的三视图如图所示,则该零件的体积为( )
 某零件的三视图如图所示,则该零件的体积为( )
某零件的三视图如图所示,则该零件的体积为( )| A. | $\frac{7}{3}$ | B. | $\frac{8-π}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{7-π}{3}$ |
2.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x-1}-2,x≥1}\\{{2}^{1-x}-2,x<1}\end{array}\right.$,则不等式f(x-1)≤0的解集为( )
| A. | {x|0≤x≤2} | B. | {x|0≤x≤3} | C. | {x|1≤x≤2} | D. | {x|1≤x≤3} |