题目内容
 给出x的8个值:5,1,0.5,-3,6,0,-2,8.执行如图所示的程序后,输出的数构成的集合为A.
给出x的8个值:5,1,0.5,-3,6,0,-2,8.执行如图所示的程序后,输出的数构成的集合为A.(1)试用列举法表示集合A;
(2)若a∈A,试比较log0.5a,log3a,lga的大小.
考点:伪代码,集合的表示法,对数值大小的比较
专题:函数的性质及应用
分析:(1)利用伪代码,判断给出x的8个值,保留大于1的数值,写出集合A即可.
(2)利用集合A,分别判断第三者的大小即可.
(2)利用集合A,分别判断第三者的大小即可.
解答:
解:(1)给出x的8个值:5,1,0.5,-3,6,0,-2,8.执行如图所示的程序后,输出结果是大于1的数值,所以A={5,6,8}.
(2)当a=5,6,8时,log0.5a<0,0<lga<log3a,
所以log0.5a<lga<log3a.
(2)当a=5,6,8时,log0.5a<0,0<lga<log3a,
所以log0.5a<lga<log3a.
点评:本题考查伪代码以及程序框图的应用,对数值的大小比较,考查计算能力.

练习册系列答案
相关题目
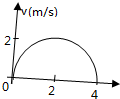 如图所示,一个物体在4s内的速度图象恰好时一个半圆,以下关于物体的运动的说法正确的是( )
如图所示,一个物体在4s内的速度图象恰好时一个半圆,以下关于物体的运动的说法正确的是( )| A、物体前2s作匀加速直线运动,后2s作匀减速直线运动 |
| B、物体在前2s作加速度越来越小的加速运动,后2s作加速度越来越大的减速运动 |
| C、物体在4s内的位移大小是2π(m) |
| D、物体在4s内的位移大小无法确定 |
已知函数f(x)=ex-x2,若?x∈[1,2],不等式-m≤f(x)≤m2-4恒成立,则实数m的取值范围是( )
| A、(-∞,1-e] |
| B、[1-e,e] |
| C、[-e,e+1] |
| D、[e,+∞) |
如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则几何体的表面积为( )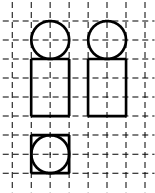

| A、32+4π | ||
| B、24+4π | ||
C、12+
| ||
D、24+
|
函数f(x)=log2(x+1)-
的零点的个数是( )
| 2 |
| x |
| A、0 | B、1 | C、2 | D、3 |