题目内容
16.用秦九韶算法求f(x)=3x5+8x4-3x3+5x2+12x-6,当x=2时,V3的值为( )| A. | 55 | B. | 56 | C. | 57 | D. | 58 |
分析 先将多项式改写成如下形式:f(x)=((((3x+8)x-3)x+5)x+12)x-6,将x=2代入并依次计算v0,v1,v2,v3的值,即可得到答案.
解答 解:多项式f(x)=3x5+8x4-3x3+5x2+12x-6=((((3x+8)x-3)x+5)x+12)x-6,
当x=2时,
v0=3,
v1=14,
v2=25,
v3=55,
故选A
点评 本题考查的知识点是秦九韶算法,其中熟练掌握秦九韶算法的运算法则,是解答本题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
11.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的离心率为2,则$\frac{b}{a}$等于( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
8.点(1,2)到直线y=x-2的距离为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $3\sqrt{2}$ |
5.$\sqrt{co{s}^{2}201.2°}$可化为( )
| A. | cos201.2° | B. | -cos201.2° | C. | sin201.2° | D. | tan201.2° |
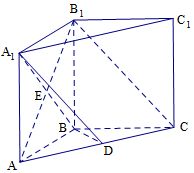 如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD;
如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD;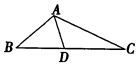 如图所示,D为△ABC中边BC上的一点,∠CAD=∠B,若AD=6,AB=8,BD=7,求DC的长.
如图所示,D为△ABC中边BC上的一点,∠CAD=∠B,若AD=6,AB=8,BD=7,求DC的长.