题目内容
1.如图所示,小波从A街区开始向右走,在每个十字路口都会遇到红绿灯,要是遇到绿灯则小波继续往前走,遇到红灯就往回走,假设任意两个十字路口的绿灯亮或红灯亮都是相互独立的,且绿灯亮的概率都是$\frac{2}{3}$,红灯亮的概率都是$\frac{1}{3}$.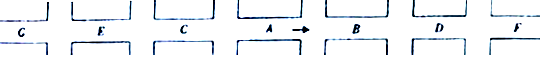
(1)求小波遇到4次红绿灯后,处于D街区的概率;
(2)若小波一共遇到了3次红绿灯,设此时小波所处的街区与A街区相距的街道数为ξ(如小波若处在A街区则相距零个街道,处在D,E街区都是相距2个街道),求ξ的分布列和数学期望.
分析 (1)设小波遇到4次绿灯之后处于D街区为事件A,则事件A共有三个基本事件,由此能求出小波遇到4次绿灯后,处于D街区的概率.
(2)ξ可能的取值为0,1,2,3,分别求出相应的概率,由此能求出ξ分布列和数学期望.
解答 解:(1)设小波遇到4次红绿灯之后处于D街区为事件A,
则事件A共有三个基本事件,
即四次遇到的红绿灯情况分别为{红红绿绿,绿红红绿,绿绿红红}.
故$P(A)=3×{(\frac{2}{3})^2}×{(\frac{1}{3})^2}=\frac{4}{27}$.
(2)ξ可能的取值为0,1,2,3,
$P(ξ=0)={(\frac{1}{3})^3}+\frac{2}{3}×\frac{1}{3}×\frac{2}{3}=\frac{5}{27}$,
$P(ξ=1)=\frac{2}{3}×\frac{1}{3}×\frac{1}{3}+\frac{1}{3}×\frac{1}{3}×\frac{2}{3}+\frac{1}{3}×\frac{2}{3}×\frac{1}{3}=\frac{6}{27}$,
$P(ξ=1)=\frac{2}{3}×\frac{2}{3}×\frac{1}{3}+\frac{1}{3}×\frac{2}{3}×\frac{2}{3}=\frac{8}{27}$,
$P(ξ=3)={(\frac{2}{3})^3}=\frac{8}{27}$.
故分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{5}{27}$ | $\frac{6}{27}$ | $\frac{8}{27}$ | $\frac{8}{27}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.若x>2m2-3是-1<x<4的必要不充分条件,则实数m的取值范围是( )
| A. | [-3,3] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | [-1,1] |
16.用秦九韶算法求f(x)=3x5+8x4-3x3+5x2+12x-6,当x=2时,V3的值为( )
| A. | 55 | B. | 56 | C. | 57 | D. | 58 |
11.抛物线y2=12x的准线与双曲线$\frac{x^2}{4}-\frac{y^2}{12}=1$的两条渐近线围成的三角形的面积为( )
| A. | 6 | B. | $6\sqrt{3}$ | C. | 9 | D. | $9\sqrt{3}$ |
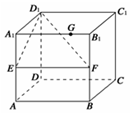 在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$.
在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$.