题目内容
在直角坐标系xOy中,直线l的方程为:
(t为参数),曲线C的参数方程为
(α为参数).
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,
),判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离d的最小值以及取到最小值时所对应的点Q的坐标.
|
|
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,
| π |
| 2 |
(2)设点Q是曲线C上的一个动点,求它到直线l的距离d的最小值以及取到最小值时所对应的点Q的坐标.
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(1)求出点P的直角坐标,代入方程,即可判断点P与直线l的位置关系;
(2)设点Q的坐标为(
cosα,sinα),求出点Q到直线l的距离,即可得出结论.
(2)设点Q的坐标为(
| 3 |
解答:
解:(1)把极坐标系下的点P(4,
),化为直角坐标,得P(0,4).
因为点P的直角坐标(0,4)满足直线l的方程x+y=4,所以点P在直线l上.
(2)因为点Q在曲线C上,故可设点Q的坐标为(
cosα,sinα),
从而点Q到直线l的距离为:d=
=
≥
所以d 的最小值为
.此时sin(α+
)=1,从而可以取α=
.
于是有:
.所以点Q的坐标为:Q(
,
).
| π |
| 2 |
因为点P的直角坐标(0,4)满足直线l的方程x+y=4,所以点P在直线l上.
(2)因为点Q在曲线C上,故可设点Q的坐标为(
| 3 |
从而点Q到直线l的距离为:d=
|
| ||
|
|4-2sin(α+
| ||
|
| 2 |
所以d 的最小值为
| 2 |
| π |
| 3 |
| π |
| 6 |
于是有:
|
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查把极坐标方程化为直角坐标方程、把参数方程化为普通方程的方法,点到直线的距离公式的应用,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
点F为双曲线
-
=1(a>0,b>0)的左焦点,过F的直线l交双曲线右支于点E,若圆x2+y2=
上一点P满足
+
=2
,且∠FOP为锐角,则该双曲线的离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
| OF |
| OE |
| OP |
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|

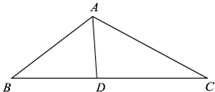 若可变形的三角形模型在变换过程中三角形周长和面积可同时取得最小值(或最大值),则称此模型为“周积三角形”.某模型厂家用一根定长连接杆AD,两根单向伸缩连接杆AB、AC(A端固定,B、C端可伸缩)以及一根双向伸缩连接杆BC制作了如图所示的可变三角形模型(所有连接杆均为笔直的金属杆).模型中,双向伸缩杆BC用一个活动连接装置固定在D点,使BC可在D处自由转动.已知:模型中,∠BAD=∠CAD=60°,AD=1分米,AB和AC最多可伸长到5分米,BC的双向伸缩能力均很强.设AB=x分米,AC=y分米.
若可变形的三角形模型在变换过程中三角形周长和面积可同时取得最小值(或最大值),则称此模型为“周积三角形”.某模型厂家用一根定长连接杆AD,两根单向伸缩连接杆AB、AC(A端固定,B、C端可伸缩)以及一根双向伸缩连接杆BC制作了如图所示的可变三角形模型(所有连接杆均为笔直的金属杆).模型中,双向伸缩杆BC用一个活动连接装置固定在D点,使BC可在D处自由转动.已知:模型中,∠BAD=∠CAD=60°,AD=1分米,AB和AC最多可伸长到5分米,BC的双向伸缩能力均很强.设AB=x分米,AC=y分米.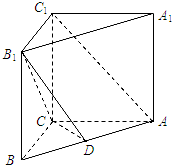 如图,直三棱柱ABC-1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.
如图,直三棱柱ABC-1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.