题目内容
12.$\overrightarrow{a}$=(2cos$\frac{π}{4}$x,1),$\overrightarrow{b}$=(sin($\frac{π}{2}$+$\frac{π}{4}$x),-1)定义在R上的函数f(x+1)=-f(x),∈[1,3]时,f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$则下列大小关系正确的是( )| A. | f(tan($\frac{1}{2}π-1$))>f(cot1) | B. | f(cos$\frac{5}{6}π$)$<f(cos\frac{π}{3})$ | C. | f(sin2)>f(cos2) | D. | f(cos1)>f(sin1) |
分析 根据函数性质得出函数周期,作出函数的图形草图,根据函数的单调性与对称性判断.
解答 解:∵f(x+1)=-f(x),
∴f(x)=-f(x-1),f(x)=-f(x+1),
∴f(x-1)=f(x+1).
∴f(x)是周期为2的函数.
当x∈[1,3]时,f(x)=$\overrightarrow{a}•\overrightarrow{b}$=2cos$\frac{πx}{4}$sin($\frac{π}{2}+\frac{πx}{4}$)-1=2cos2$\frac{πx}{4}$-1=cos$\frac{πx}{2}$.
∴f(x)在[1+2k,2+2k]上单调递减,在[2+2k,3+2k]上单调递增,
作出f(x)的图象草图: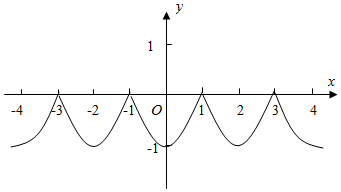
由图象可知f(x)为偶函数.
对于A,∵tan($\frac{π}{2}-1$)=cot1,∴f(tan($\frac{π}{2}-1$))=f(cot1).故A错误.
f(cos$\frac{5π}{6}$)=f(-$\frac{\sqrt{3}}{2}$)=f($\frac{\sqrt{3}}{2}$),f(cos$\frac{π}{3}$)=f($\frac{1}{2}$),
对于B,∵$0<\frac{1}{2}<\frac{\sqrt{3}}{2}<1$,∴f($\frac{1}{2}$)<f($\frac{\sqrt{3}}{2}$),即f(cos$\frac{5π}{6}$)>f(cos$\frac{π}{3}$),故B错误.
对于D,∵1>sin1>cos1>0,
∴f(sin1)>f(cos1),故D错误.
故选:C.
点评 本题考查了函数的周期性应用,向量数量积的运算,余弦函数的图象与性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知tan(α-$\frac{π}{4}$)=$\frac{1}{2}$,则$\frac{sinα+cosα}{sinα-cosα}$的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | -2 |