题目内容
3.在气象台A正东方向400千米的B处海面上有一个台风中心形成.已知台风以每小时40千米的速度向西北方向移动,距台风中心300千米以内的地方都会受到台风的影响,问从现在起多少时间气象台A会受到台风影响,持续影响的时间有多长?分析 作出图形,使用余弦定理求出台风中心距A300千米时的时间,则两根之差为台风持续时间.
解答 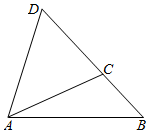 解:设t小时后A地会受到台风影响,台风中心为C,则BC=40t,
解:设t小时后A地会受到台风影响,台风中心为C,则BC=40t,
在△ABC中,AB=400,AC=300,BC=40t,B=45°,
由余弦定理得cosB=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•BC}$=$\frac{70000+1600{t}^{2}}{32000t}$=$\frac{\sqrt{2}}{2}$,
解得t1=5$\sqrt{2}-$$\frac{5}{2}$,t2=5$\sqrt{2}$$+\frac{5}{2}$,
∴t2-t1=5.
∴问从现在起5$\sqrt{2}$-$\frac{5}{2}$小时后气象台A会受到台风影响,持续影响的时间为5小时.
点评 本题考查了解三角形的实际应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.在△ABC中,角A,B,C所对的边分别为a,b,c,且b=2$\sqrt{2}$,a=2,若三角形有解,则角A的范围是( )
| A. | (0,$\frac{π}{6}$] | B. | (0,$\frac{π}{4}$] | C. | (0,$\frac{π}{3}$] | D. | (0,$\frac{π}{2}$] |
12.$\overrightarrow{a}$=(2cos$\frac{π}{4}$x,1),$\overrightarrow{b}$=(sin($\frac{π}{2}$+$\frac{π}{4}$x),-1)定义在R上的函数f(x+1)=-f(x),∈[1,3]时,f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$则下列大小关系正确的是( )
| A. | f(tan($\frac{1}{2}π-1$))>f(cot1) | B. | f(cos$\frac{5}{6}π$)$<f(cos\frac{π}{3})$ | C. | f(sin2)>f(cos2) | D. | f(cos1)>f(sin1) |
13.在△ABC中,角A、B、C所对的边分别为a、b、c,如果$\frac{a}{b}$=2$\sqrt{3}$cos(B+C),B=30°,那么角A等于( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |