题目内容
9.已知p:-2≤x≤10,q:x2-2x+1-m2≤0(m>0),若¬p是¬q的必要非充分条件,求实数m的取值范围.分析 求出不等式对应的等价条件,利用充分条件和必要条件的定义建立条件关系即可得到结论.
解答 解:∵¬p是¬q的必要非充分条件,
∴q是p的必要非充分条件,即p是q的充分不必要条件.
由x2-2x+1-m2≤0,得1-m≤x≤1+m,m>0.
要使p是q的充分不必要条件,
则$\left\{\begin{array}{l}{m>0}\\{1-m<-2}\\{1+m≥10}\end{array}\right.$,或$\left\{\begin{array}{l}{m>0}\\{1-m≤-2}\\{1+m>10}\end{array}\right.$,得m≥9,
∴实数m的取值范围是m≥9.
点评 本题主要考查充分条件和必要条件的应用,利用逆否命题的等价性进行转化是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.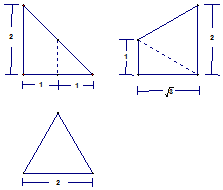 如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )
如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )
 如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )
如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
4.圆x2+y2=1与圆(x-2)2+(y-2)2=5的位置关系为( )
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 相离 |
14.若直线$\sqrt{3}x-2y=0$与圆(x-4)2+y2=r2(r>0)相切,则r=( )
| A. | $\frac{48}{7}$ | B. | 5 | C. | $\frac{{4\sqrt{21}}}{7}$ | D. | 25 |
1.已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{3}}$f(x)的单调递增区间为( )


| A. | (-∞,0) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
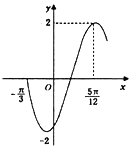 函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.
函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.