题目内容
5.将函数$y=3sin(2x+\frac{π}{6})$的图象上各点沿x轴向右平移$\frac{π}{6}$个单位长度,所得函数图象的一个对称中心为( )| A. | $(\frac{7π}{12},0)$ | B. | $(\frac{π}{6},0)$ | C. | $(\frac{5π}{8},0)$ | D. | $(\frac{2π}{3},-3)$ |
分析 根据y=Asin(ωx+∅)的图象变换规律可得所得图象对应的函数为y=3sin(2x-$\frac{π}{6}$),由2x-$\frac{π}{6}$=kπ,k∈z,可得对称中心的横坐标,从而得出结论.
解答 解:将函数$y=3sin(2x+\frac{π}{6})$的图象上各点沿x轴向右平移$\frac{π}{6}$个单位长度,
可得函数y=3in[2(x-$\frac{π}{6}$)+$\frac{π}{6}$]=3sin(2x-$\frac{π}{6}$)的图象,
由2x-$\frac{π}{6}$=kπ,k∈z,
可得:x=$\frac{kπ}{2}$+$\frac{π}{12}$,故所得函数图象的对称中心为($\frac{kπ}{2}$+$\frac{π}{12}$,0),k∈z.
令k=1可得一个对称中心为($\frac{7π}{12}$,0).
故选:A.
点评 本题主要考查y=Asin(ωx+∅)的图象变换规律,正弦函数的对称中心,考查了数形结合思想的应用,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
16.设函数f(x)=-|x|,g(x)=lg(ax2-4x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
| A. | (-2,0] | B. | (0,2] | C. | (-∞,4] | D. | [4,+∞) |
14.若直线$\sqrt{3}x-2y=0$与圆(x-4)2+y2=r2(r>0)相切,则r=( )
| A. | $\frac{48}{7}$ | B. | 5 | C. | $\frac{{4\sqrt{21}}}{7}$ | D. | 25 |
 如图,在三棱锥P-ABC中,PA⊥平面ABC,E,F分别为PC,PB中点,∠ACB=90°.
如图,在三棱锥P-ABC中,PA⊥平面ABC,E,F分别为PC,PB中点,∠ACB=90°.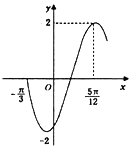 函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.
函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.