题目内容
12.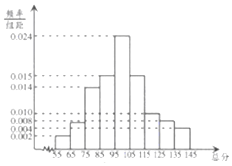 从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.
从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.(1)求这100份数学试卷的样本平均分$\overline x$和样本方差s2
(同一组中的数据用该组区间的中点值作代表)
(2)由直方图可以认为,这批学生的数学总分Z服从正态分布N(μ,σ2),其中μ近似为样本平均数$\overline x$,σ2近似为样本方差s2.
①利用该正态分布,求P(81<z<119);
②记X表示2400名学生的数学总分位于区间(81,119)的人数,利用①的结果,求EX(用样本的分布区估计总体的分布).
附:$\sqrt{366}$≈19,$\sqrt{326}$≈18,若Z=~N(μ,2),则P(μ-σ2),则P(μ-σ<Z<μ+σ)=0.6826,P(μ-2σ<Z<μ+2σ)=0.9544.
分析 (1)一组中的数据用该组区间的中点值作代表,求这100份数学试卷的样本平均分$\overline x$和样本方差s2;
(2)①利用该正态分布,Z~N(100,366),即可求P(81<z<119);
②数学总分位于区间(81,119)的概率为0.6826,X~(2400,0.6826),即可求EX.
解答 解:(1)由题意,$\overline{x}$=60×0.02+70×0.08+80×0.14+90×0.15+100×0.24+110×0.15+120×0.1+130×0.08+140×0.04=100,
样本方差s2=(60-100)2×0.02+(70-100)2×0.08+(80-100)2×0.14+(90-100)2×0.15+(100-100)2×0.24+(110-100)2×0.15+(120-100)2×0.1+(130-100)2×0.08+(140-100)2×0.04=366;
(2)Z~N(100,366),P(81<z<119)=P(100-19<z<100+19)=0.6826;
②数学总分位于区间(81,119)的概率为0.6826,X~(2400,0.6826),
EX=2400×0.6826=1638.24.
点评 本题考查频率分布直方图的应用,样本方差的求法,正态分布,考查分析问题解决问题的能力,属于中档题.

练习册系列答案
相关题目
7.函数f(x)是定义在R上的奇函数,且f(x-1)为偶函数,当x∈[0,1]时,$f(x)={x^{\frac{1}{2}}}$,若函数g(x)=f(x)-x-b恰有一个零点,则实数b的取值集合是( )
| A. | $(2k-\frac{1}{4},2k+\frac{1}{4}),k∈Z$ | B. | $(2k+\frac{1}{2},2k+\frac{5}{2}),k∈Z$ | ||
| C. | $(4k-\frac{1}{4},4k+\frac{1}{4}),k∈Z$ | D. | $(4k+\frac{1}{4},4k+\frac{15}{4}),k∈Z$ |
4.圆x2+y2=1与圆(x-2)2+(y-2)2=5的位置关系为( )
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 相离 |
1.已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{3}}$f(x)的单调递增区间为( )


| A. | (-∞,0) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
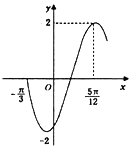 函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.
函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.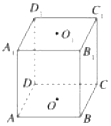 如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.
如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.