Question

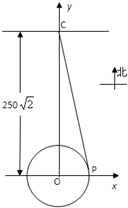某城市交通规划中，拟在以点O为圆心，半径为50m的高架圆形车道外侧P处开一个出口，以与圆形道相切的方式，引申一条直道连接到距圆形道圆心O正北250

2

m的道路上C处（如图），以O为原点，OC为y轴建立如图所示的直角坐标系，求直道PC所在的直线方程，并计算出口P的坐标．

Answer 1

考点：直线与圆的位置关系

专题：直线与圆

分析：由题意可得圆形道的方程为x²+y²=50²，点C的坐标为（0，250

2

）．根据CP与圆O相切求得CP的斜率k的值，再根据两条直线垂直的性质求得OP的斜率，可得OP的方程，再根据CP、OP的方程，求得P点坐标．

解答： 解：由题意可得圆形道的方程为x²+y²=50²，引伸道与北向道路的交接点C的坐标为（0，250

2

）．
设CP的方程为 y=kx+250

2

，由图可知k＜0．
又CP与圆O相切，∴O到CP距离

250 2

1+k2

=50，解得k=-7，
∴CP的方程为 y=-7x+250

2

 ①．
又OP⊥CP，∴K_OP•K_CP=-1，∴K_OP=-

1

KCP

=

1

7

． 则OP的方程是：y=

1

7

x ②．
由①②解得P点坐标为（35

2

，5

2

），
∴引伸道所在的直线方程为7x+y-250

2

=0，出口P的坐标是（35

2

，5

2

）．

点评：本题主要考查两条直线垂直的性质，直线和圆的位置关系，点到直线的距离公式，属于基础题．