题目内容
设（1+2x）20=（a0+a1x+a2x2+…+a9x9+a10x10）•（1+x）10+b0+b1x+b2x2+…+b9x9，则b0-b1+b2-b3+…+b8-b9= ．
考点：二项式系数的性质
专题：二项式定理
分析：通过对等式中的x赋值-1得到各项系数和；．
解答：
解：（1+2x）10=（a0+a1x+a2x2+…+a9x9+a10x10）•（1+x）10+b0+b1x+b2x2+…+b9x9
令x=-1，得b0-b1+b2-b3+…-b9=1
故答案为：1．
令x=-1，得b0-b1+b2-b3+…-b9=1
故答案为：1．
点评：本题考查通过赋值求展开式的系数和．
练习册系列答案
相关题目
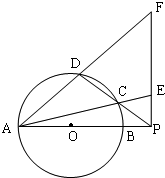如图，圆O的直径AB=10，P是AB延长线上一点，BP=2，割线PCD交圆O于点C，D，过点P做AP的垂线，交直线AC于点E，交直线AD于点F．（1）求证：∠PEC=∠PDF；
（2）求PE•PF的值．
设集合A={x|1＜x＜5}，B={x|x2-2x-3≤0}，则A∩（∁RB）=（ ）
| A、（1，5） |
| B、（3，5） |
| C、（1，3） |
| D、（1，2） |