题目内容

若a，b，c为有理数，且等式a+b
32
+c
34
=0成立，则a=b=c=0．
考点：反证法与放缩法
专题：证明题,反证法
分析：假设a，b，c至少有一个不为0，则分类讨论，引出矛盾，即可得出结论．
解答： 证明：假设a，b，c至少有一个不为0，则
①a=b=0，c≠0，等式a+b
32
+c
34
=0不成立；
②a≠0，b=0，c≠0，等式a+b
32
+c
34
=0为a+c
34
=0，∴
34
=-
a
c
，
∵a，c为有理数，∴
34
=-
a
c
不成立．
∴a=b=c=0．
点评：本题考查反证法，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
某班同学进行了一次数学测试，将所得的数据整理后，画出频率分布直方图，已知图中从左到右的前三个小组的频率分别是0.1，0.3，0.4，且第一小组的频数是5．
（Ⅰ）求第四小组的频率和本班学生人数；
（Ⅱ）在这次测试中，全班成绩的中位数会落在第几小组内？
（Ⅲ）若本次测试成绩达到100分为优秀，试估计本班优秀率是多少？
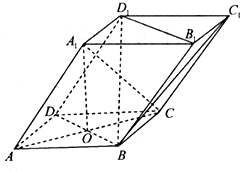如图，四棱柱ABCD-A1B1C1D1的底面ABCD是菱形，AC，BD交于点O，A1O⊥平面ABCD，A1A=BD=2，AC=2
2
．
（1）证明：A1C⊥平面BB1D1D；
（2）求平面BC1D1与平面BB1D1D夹角的余弦值．
如图，在四棱柱ABCD=A1B1C1D1中，侧棱AA1⊥底面ABCD，DC=DD1=2AD=2AB=2，AD⊥DC，AB∥DC．
（1）求四棱柱ABCD-A1B1C1D1的体积；    
（2）求证：D1C⊥AC1；
（3）设F是BC上一点，试确定F的位置，使D1F∥平面A1BD，并说明理由．
已知函数y=f（x）满足
a
=(x2，y)，
b
=(x-
1
x
，-1)，且
a
•
b
=-1．如果存在正项数列{an}满足：a1=
1
2
，
n
i=1
f(ai)-n=
n
i=1
ai3-n2an(n∈N*)．
（1）求数列{an}的通项；
（2）证明：
n
i=1
ai
i
＜3．
已知等差数列{an}的公差d≠0，首项a1=3，且a1、a4、a13成等比数列，设数列{an}的前n项和为Sn（n∈N+）．
（1）求an和Sn；
（2）若bn=
an(n≤4且n∈N+)
1
Sn
(n≥5且n∈N+)
，求数列{bn}的前n项和Tn．
将圆周上5个点按如下规则染色：先任选一点染成红色，然后依逆时针方向，第1步转过1个间隔将到达的那个点染红，第2步转过2个间隔将到达的那个点染红，第k步转过k个间隔将到达的那个点染红．一直进行下去，可得到
个红点．
在二维平面向量加法运算中：若
a
=（x1，y1），
b
=（x2，y2），则
a
+
b
=（x1+x2，y1+y2）．若类比到空间三维向量的加法运算：若
a
=（x1，y1，z1），
b
=（x2，y2，z2），则
a
+
b
=
 
．
已知函数f（x）=
ax(x＞0)
(2-a)x+
2
3
a(x≤0)
在R上为增函数，则a的取值范围是
 
（用区间表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网