题目内容
已知cosθ=-
,
<θ<3π,那么sin
等于( )
| 1 |
| 5 |
| 5π |
| 2 |
| θ |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点:半角的三角函数
专题:三角函数的求值
分析:
<θ<3π⇒
<
<
⇒sin
<0,再利用cosθ=1-2sin2
=-
,即可求得答案.
| 5π |
| 2 |
| 5π |
| 4 |
| θ |
| 2 |
| 3π |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| 1 |
| 5 |
解答:
解:∵
<θ<3π,
∴
<
<
,
∴sin
<0;①
又cosθ=1-2sin2
=-
,
∴sin2
=
;②
由①②得:sin
=-
,
故选:A.
| 5π |
| 2 |
∴
| 5π |
| 4 |
| θ |
| 2 |
| 3π |
| 2 |
∴sin
| θ |
| 2 |
又cosθ=1-2sin2
| θ |
| 2 |
| 1 |
| 5 |
∴sin2
| θ |
| 2 |
| 3 |
| 5 |
由①②得:sin
| θ |
| 2 |
| ||
| 5 |
故选:A.
点评:本题考查半角的三角函数,确定sin
<0是关键,考查运算求解能力,属于中档题.
| θ |
| 2 |

练习册系列答案
相关题目
已知点M1(4,2),M2(1,8),
=
,则点M的坐标为( )
| M1M |
| 1 |
| 2 |
| MM2 |
| A、(2,5) |
| B、(3,2) |
| C、(4,3) |
| D、(3,4) |
从(
+
)20的展开式中任取一项,则取到有理项的概率为( )
| 4 | x |
| 1 | ||
|
A、
| ||
B、
| ||
C、
| ||
D、
|
方程x3-x-1=0仅有一个正实数解x,则x∈( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
曲线y=2x2在点P(2,8)处的切线方程为( )
| A、8x+y-8=0 |
| B、8x-y-8=0 |
| C、x+8y-8=0 |
| D、x-y+8=0 |
如图是导函数y=f′(x)的图象,那么函数y=f(x)在区间[a,b]内的极值点有( )
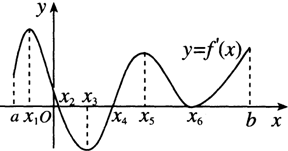

| A、0 | B、1 | C、2 | D、3 |
若大前提是:任何实数的平方都大于0,小前提是:a∈R,结论是:a2>0,那么这个演绎推理所得结论错误的原因是( )
| A、小前提错误 |
| B、大前提错误 |
| C、推理形式错误 |
| D、大前提小前提都错 |