题目内容
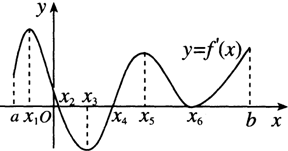
如图是导函数y=f′（x）的图象，那么函数y=f（x）在区间[a，b]内的极值点有（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：利用导数研究函数的极值
专题：导数的概念及应用
分析：结合函数的图象，得到函数的单调区间，从而求出函数的极值点．
解答：
解：由题意得：f（x）在（a，x2）递增，在（x2，x4）递减，在（x4，b）递增，
∴函数f（x）在x=x2，x=x4处有极值，
故选：C．
∴函数f（x）在x=x2，x=x4处有极值，
故选：C．
点评：本题考查了函数的单调性，函数的极值问题，考查导数的应用，数形结合思想，是一道基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
S是△ABC所在平面外一点，SA=SB=SC，则S在平面ABC内的射影O是△ABC的（ ）
| A、内心 | B、外心 | C、重心 | D、垂心 |
已知复数z=1+2i，则
=（ ）
| 1 |
| z |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
设集合I={0，1，2，3，4，5}．选择I的两个非空子集A和B，要使B中最小的数大于A中最大的数，则不同的选择方法共有（ ）
| A、49种 | B、50种 |
| C、129种 | D、130种 |
已知cosθ=-
，
＜θ＜3π，那么sin
等于（ ）
| 1 |
| 5 |
| 5π |
| 2 |
| θ |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
已知平面向量
，
，
满足|
|=1，|
|=2，|
|=3，且
，
，
两两所成的角相等，则|
+
+
|等于（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
A、
| ||
| B、6 | ||
C、6或
| ||
D、6或
|
角α的终边上有一点P（a，a），a∈R，a≠0，则tanα的值是（ ）
A、
| ||||||||
B、-
| ||||||||
C、
| ||||||||
| D、1 |