题目内容
2.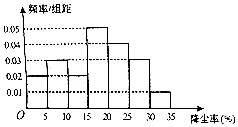 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:若降尘率达到18%以上,则认定雾炮除尘有效.
(1)根据以上数据估计雾炮除尘有效的概率;
(2)现把A市规划成三个区域,每个区域投放3台雾炮进行除尘(雾炮之间工作互不影响),若在一个区域内的3台雾炮降尘率都低于18%,则需对该区域后期追加投入20万元继续进行治理,求后期投入费用的分布列和期望.
分析 (1)估计雾炮除尘有效的概率P=$\frac{2}{5}×$5×0.05+5×0.04+5×0.03+5×0.01.
(2)由(1)可得:在一个区域内的3台雾炮降尘率都低于18%,则需对该区域后期追加投入20万元继续进行治理,
因此在一个区域内需对该区域后期追加投入20万元继续进行治理的概率P=$(\frac{1}{2})^{3}$=$\frac{1}{8}$.后期投入区域X~B$(3,\frac{1}{8})$.后期投入费用ξ=20X(万元).利用P(ξ=20k)=P(X=k)=${∁}_{3}^{k}(\frac{1}{8})^{k}(1-\frac{1}{8})^{3-k}$即可得出.
解答 解:(1)估计雾炮除尘有效的概率P=$\frac{2}{5}×$5×0.05+5×0.04+5×0.03+5×0.01=$\frac{1}{2}$.
(2)由(1)可得:在一个区域内的3台雾炮降尘率都低于18%,则需对该区域后期追加投入20万元继续进行治理,
因此在一个区域内需对该区域后期追加投入20万元继续进行治理的概率P=$(\frac{1}{2})^{3}$=$\frac{1}{8}$.
∴后期投入区域X~B$(3,\frac{1}{8})$.后期投入费用ξ=20X(万元).
P(ξ=20k)=P(X=k)=${∁}_{3}^{k}(\frac{1}{8})^{k}(1-\frac{1}{8})^{3-k}$.
ξ的分布列为:
| ξ | 0 | 20 | 40 | 60 |
| P | $\frac{343}{512}$ | $\frac{147}{512}$ | $\frac{21}{512}$ | $\frac{1}{512}$ |
点评 本题考查了频率分布直方图的性质、二项分布列与数学期望计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
12.在△ABC中,三个内角∠A,∠B,∠C所对的边分别为a,b,c,且A:B:C=1:2:3,则a:b:c=( )
| A. | 3:2:1 | B. | 2:$\sqrt{3}$:1 | C. | 1:2:3 | D. | 1:$\sqrt{3}$:2 |
10.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>1}\\{(\frac{1}{2})^{x},x≤1}\end{array}\right.$,则f(f(-$\frac{1}{2}$))=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
7.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1的焦点到其渐近线的距离为( )
| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | 4 |
14.下列关系中,正确的是( )
| A. | $\sqrt{2}$∈N | B. | $\frac{1}{2}$∈Z | C. | ∅?{0,1} | D. | $\frac{1}{2}$∉Q |