题目内容
7.已知x2+y2≤1,则|x2+2xy-y2|的最大值为$\sqrt{2}$.分析 由实数x、y满足x2+y2≤1,利用三角函数代换x=cosθ,y=sinθ,结合三角函数知识即可得出.
解答 解:∵实数x、y满足x2+y2≤1,
∴可设x=cosθ,y=sinθ(θ∈[0,2π)),
|x2+2xy-y2|=|cos2θ+sin2θ|=|$\sqrt{2}$sin(2θ+$\frac{π}{4}$)|≤$\sqrt{2}$,当且仅当|sin(2θ+$\frac{π}{4}$)|=1,取得最大值.
故答案为:$\sqrt{2}$.
点评 本题考查了圆的参数方程、三角函数代换、三角函数基本关系式等基础知识与基本技能方法,考查了转化方法和计算能力,属于中档题.

练习册系列答案
相关题目
15.已知圆C:(x-1)2+(y-2)2=25及直线l:(2m+1)x+(m+1)y=7m+4(m∈R),则直线l过的定点及直线与圆相交得的最短弦长分别为( )
| A. | (3,1),$4\sqrt{5}$ | B. | (2,1),$4\sqrt{5}$ | C. | (-3,1),$4\sqrt{3}$ | D. | (2,-1),3$\sqrt{3}$ |
2.已知集合A={x|log${\;}_{\frac{1}{2}}$(x+1)≥-2},B={x|$\frac{x+2}{1-x}$≥2},则 A∩B=( )
| A. | (-1,1) | B. | [0,1) | C. | [0,3] | D. | ∅ |
12.在△ABC中,三个内角∠A,∠B,∠C所对的边分别为a,b,c,且A:B:C=1:2:3,则a:b:c=( )
| A. | 3:2:1 | B. | 2:$\sqrt{3}$:1 | C. | 1:2:3 | D. | 1:$\sqrt{3}$:2 |
19.已知函数$f(x)=\left\{\begin{array}{l}{x^2}-x,x≤0\\-{2^x},x>0\end{array}\right.$,则“f(x)≤0”是“x=0”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
16.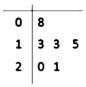 如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )
如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )
 如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )
如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )| A. | 中位数为14 | B. | 众数为13 | C. | 平均数为15 | D. | 方差为19 |