若抛物线y=$\frac{1}{4}$x2上一点P到焦点F的距离为5.则P点的坐标是( )A．B．C．(±$\frac{79}{16}$.$\frac{\sqrt{79}}{8}$)D．(±$\frac{\sqrt{79}}{8}$.$\frac{79}{16}$) 题目和参考答案——青夏教育精英家教网—

题目内容

4．若抛物线y=$\frac{1}{4}$x²上一点P到焦点F的距离为5，则P点的坐标是（　　）

A．

（4，±4）

B．

（±4，4）

C．

（±$\frac{79}{16}$，$\frac{\sqrt{79}}{8}$）

D．

（±$\frac{\sqrt{79}}{8}$，$\frac{79}{16}$）

分析利用抛物线的性质，求出P的纵坐标，然后求解横坐标即可．

解答解：抛物线y=$\frac{1}{4}$x²上一点P到焦点F的距离为5，可得抛物线的准线方程为：y=-1，
则P的纵坐标为：4，则x²=16，解得x=±4．
则P点的坐标是：（±4，4）．
故选：B．

点评本题考查抛物线的简单性质的应用，考查计算能力．

练习册系列答案

	A．	充分不必要条件		B．	必要不充分条件
	C．	充分必要条件		D．	既不充分又不必要条件

15．已知圆C：（x-1）²+（y-2）²=25及直线l：（2m+1）x+（m+1）y=7m+4（m∈R），则直线l过的定点及直线与圆相交得的最短弦长分别为（　　）

12．在△ABC中，三个内角∠A，∠B，∠C所对的边分别为a，b，c，且A：B：C=1：2：3，则a：b：c=（　　）

19．已知函数$f（x）=\left\{\begin{array}{l}{x^2}-x，x≤0\\-{2^x}，x＞0\end{array}\right.$，则“f（x）≤0”是“x=0”的（　　）条件．

	A．	充分不必要		B．	必要不充分
	C．	充要		D．	既不充分也不必要

9．已知函数f（x）=$\frac{lnx}{x}$-$\frac{k}{x}$（k∈R）．
（1）若曲线y=f（x）在点（1，f（1））处的切线斜率为10，求函数f（x）的最大值；
（2）若不等式x²f（x）+$\frac{1}{x+1}$≥0与k≥$\frac{1}{2}$x²+（e²-2）x-e^x-7在[1，+∞）上均恒成立，求实数k的取值范围．

16．

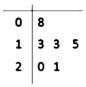如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图，则下列关于该运动员所得分数的说法错误的是（　　）

13．若f（x）=x-1-alnx（a∈R），g（x）=$\frac{{e}^{x}}{x}$
（1）当a=$\frac{1}{e}$时，求函数f（x）的最值；
（2）当a＜0时，且对任意的x₁，x₂∈[4，5]（x₁≠x₂），|f（x₁）-f（x₂）|＜|g（x₁）-g（x₂）|恒成立，求实数a的取值范围．

试题分类