题目内容
2.四棱锥M-EFGH的直观图和三视图如下: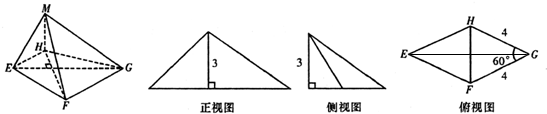
试根据三视图提供的数据和边角关系,解决如下问题:
(1)求证:MF⊥EG;
(2)求二面角M-GF-H的正切值.
分析 (1)证明EG⊥平面MHF,即可证明:MF⊥EG;
(2)过H作HA⊥FG,连接MA,则MA⊥FG,∠MAH为二面角M-GF-H的平面角,求出HA,即可求二面角M-GF-H的正切值.
解答 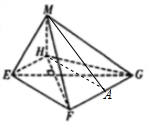 (1)证明:由三视图可得MH⊥平面EFGH,EFGH是菱形,
(1)证明:由三视图可得MH⊥平面EFGH,EFGH是菱形,
∴MH⊥EG,HF⊥EG,
∵MH∩HF=H,
∴EG⊥平面MHF,
∴MF⊥EG;
(2)解:过H作HA⊥FG,连接MA,则MA⊥FG,∠MAH为二面角M-GF-H的平面角.
∵△GHF是边长为3的等边三角形,
∴HA=$\frac{3\sqrt{3}}{2}$,
∴二面角M-GF-H的正切值=$\frac{3}{\frac{3\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查线面垂直的判定与性质,考查面面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
14.已知数列{an}满足an=$\left\{\begin{array}{l}{(5-a)n-11,n≤5}\\{{a}^{n-4},n>5}\end{array}\right.$,且{an}是递增数列,则实数a的取值范围是( )
| A. | (1,5) | B. | ($\frac{7}{3}$,5) | C. | [$\frac{7}{3}$,5) | D. | (2,5) |
12.${∫}_{0}^{π}$(cosx+2)dx等于( )
| A. | 2π | B. | 0 | C. | π+2 | D. | 1 |
14.设命题p:f(x)=lnx+x2+ax+1在(0,+∞)内单调递增,命题q:a≥-2,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
12.在△ABC中,三个内角∠A,∠B,∠C所对的边分别为a,b,c,且A:B:C=1:2:3,则a:b:c=( )
| A. | 3:2:1 | B. | 2:$\sqrt{3}$:1 | C. | 1:2:3 | D. | 1:$\sqrt{3}$:2 |
 已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为$\frac{1+sinα}{1-sinα}$.
已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为$\frac{1+sinα}{1-sinα}$.