题目内容
6.已知在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴,建立极坐标系.曲线C1的极坐标方程为ρ=4cosθ,直线l:$\left\{\begin{array}{l}x=1-\frac{{2\sqrt{5}}}{5}t\\ y=1+\frac{{\sqrt{5}}}{5}t\end{array}\right.$(t为参数).(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为$\left\{\begin{array}{l}x=2cosα\\ y=sinα\end{array}\right.$(α为参数),曲线C1上点P的极角为$\frac{π}{4}$,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
分析 (1)利用三种方程的转化方法,求曲线C1的直角坐标方程及直线l的普通方程;
(2)$P(\frac{π}{4},2\sqrt{2})$,直角坐标为(2,2),$Q(2cosα,sinα),M(1+cosα,1+\frac{1}{2}sinα)$,利用点到直线l的距离公式能求出点M到直线l的最大距离.
解答 解:(1)由曲线C1的极坐标方程为ρ=4cosθ,得直角坐标方程${C_1}:{x^2}+{y^2}-4x=0$,
直线l:$\left\{\begin{array}{l}x=1-\frac{{2\sqrt{5}}}{5}t\\ y=1+\frac{{\sqrt{5}}}{5}t\end{array}\right.$,消去参数,可得普通方程l:x+2y-3=0.(5分)
(2)$P(\frac{π}{4},2\sqrt{2})$,直角坐标为(2,2),$Q(2cosα,sinα),M(1+cosα,1+\frac{1}{2}sinα)$,
M到l的距离d=$\frac{|1+cosα+2+sinα-3|}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}|sin(α+\frac{π}{4})|$,从而最大值为$\frac{{\sqrt{10}}}{5}$.(10分)
点评 本小题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化,参数方程的运用.

练习册系列答案
相关题目
17.设全集U=R,集合A={x|x2-2x-3<0},B={x|x-1≥0},则图中阴影部分所表示的集合为( )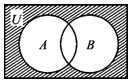

| A. | {x|x≤-1或x≥3} | B. | {x|x<1或x≥3} | C. | {x|x≤1} | D. | {x|x≤-1} |
14.已知集合A={x|x2-2x-3<0},$B=\{\;x|\frac{1}{x}<1\;\}$,则A∩B=( )
| A. | {x|1<x<3} | B. | {x|-1<x<3} | C. | {x|-1<x<0或0<x<3} | D. | {x|-1<x<0或1<x<3} |
18.某三棱锥的三视图如图所示,则该三棱锥中最长棱的长度为( )
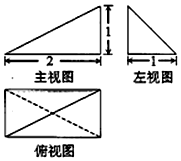

| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | 3 |