题目内容
14.已知集合A={x|x2-2x-3<0},$B=\{\;x|\frac{1}{x}<1\;\}$,则A∩B=( )| A. | {x|1<x<3} | B. | {x|-1<x<3} | C. | {x|-1<x<0或0<x<3} | D. | {x|-1<x<0或1<x<3} |
分析 先化简A,B,再求出其交集即可.
解答 解:由A={x|-1<x<3},B={x|x<0,或x>1},
故A∩B={x|-1<x<0,或1<x<3}.
故选D.
点评 本题考查了集合的交集的运算,属于基础题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
5.中国南北朝时期的著作《孙子算经》中,对同余除法有较深的研究.设a,b,m(m>0)为整数,若a和b
被m除得的余数相同,则称a和b对模m同余,记为a=b(bmodm).若$a=C_{20}^0+C_{20}^1•2+C_{20}^2•{2^2}+…+C_{20}^{20}•{2^{20}}$,a=b(bmod10),则b的值可以是( )
被m除得的余数相同,则称a和b对模m同余,记为a=b(bmodm).若$a=C_{20}^0+C_{20}^1•2+C_{20}^2•{2^2}+…+C_{20}^{20}•{2^{20}}$,a=b(bmod10),则b的值可以是( )
| A. | 2011 | B. | 2012 | C. | 2013 | D. | 2014 |
19.对函数f(x)=$\frac{cosx+m}{cosx+2}$,若?a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )
| A. | $(\;\frac{5}{4}\;,\;6\;)$ | B. | $(\;\frac{5}{3}\;,\;6\;)$ | C. | $(\;\frac{7}{5}\;,\;5\;)$ | D. | $(\;\frac{5}{4}\;,\;5\;)$ |
11.已知全集U=R,集合A={x|x2-x-6≤0},$B=\left\{{\left.x\right|\frac{4-x}{x+1}≤0}\right\}$,那么集合A∩(∁UB)=( )
| A. | [-2,4) | B. | (-1,3] | C. | [-2,-1] | D. | [-1,3] |
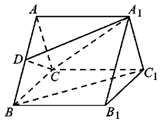 如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,侧面AA1B1B为正方形,且AA1⊥平面ABC,D为线段AB上的一点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,侧面AA1B1B为正方形,且AA1⊥平面ABC,D为线段AB上的一点.