题目内容

9．设集合A={x|-1＜x＜3}，B={x|x≥1}，则A∩B=（　　）
A．（-1，1]B．[1，3）C．[-1，3]D．（-1，+∞）

分析 由集合的交集的定义：两集合公共元素构成的集合，即可得到所求．

解答 解：集合A={x|-1＜x＜3}，B={x|x≥1}，
则A∩B={x|-1＜x＜3}∩{x|x≥1}={x|1≤x＜3}=[1，3），
故选：B．

点评 本题考查集合的交集的求法，注意运用定义法，考查运算能力，属于基础题．

练习册系列答案
相关题目
19．已知集合A={x|x2-x-2≤0}，集合B={x|m≤x＜m+5，m∈R}．
（Ⅰ）若m=0，求A∩B．
（Ⅱ）若A∩B=∅，求实数m的取值范围．
20．随机变量X的分布列如下表，且E（X）=2，则D（2X-3）=（　　）
X02a
P$\frac{1}{6}$p$\frac{1}{3}$
A．2B．3C．4D．5
17．如图，一直角墙角，两边的长度足够长，若P处有一棵树与两墙的距离分别是2m和αm（0＜α＜10），不考虑树的粗细，现用12m长的篱笆，借助墙角围成一个矩形花圃ABCD，设此矩形花圃的最大面积为u，若将这棵树围在矩形花圃内，则函数u=f（a）（单位：m2）的图象大致是（　　）
A．B．
C．D．
4．若非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|，则向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为0°．
14．定义在R上的偶函数f（x）满足f（1-x）=f（1+x），且当x∈[0，1]时，f（x）=$\sqrt{2x-{x}^{2}}$．则直线x-4y+2=0与曲线y=f（x）的交点个数为（　　）
A．3B．4C．5D．6
1．已知ξ～N（1，62），且P（-2≤ξ≤1）=0.4，则P（ξ＞4）等于（　　）
A．0.1B．0.2C．0.6D．0.8
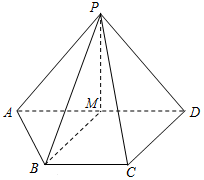18．如图，在四棱锥P-ABCD中，M为AD的中点．
（1）若AD∥BC，AD=2BC，求证：BM∥平面PCD；
（2）若PA=PD，平面PAD⊥平面PBM，求证：AD⊥PB．
9．已知$sinα=\frac{1-m}{1+m}，cosα=-\frac{3}{5}$，则m=$\frac{1}{9}$或9．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网