题目内容
7.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{2}$=1(a>0)和抛物线y2=8x有相同的焦点,则双曲线的离心率为$\sqrt{2}$.分析 求出抛物线的焦点坐标,得到双曲线的焦点坐标,列出方程求解即可得到a,然后求解离心率.
解答 解:抛物线y2=8x的焦点(2,0),则双曲线的焦点坐标(2,0),可得a2+2=4,
解得a=$\sqrt{2}$,
双曲线的离心率为:$\frac{2}{\sqrt{2}}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$
点评 本题考查双曲线以及抛物线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
 如图,一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是2m和αm(0<α<10),不考虑树的粗细,现用12m长的篱笆,借助墙角围成一个矩形花圃ABCD,设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位:m2)的图象大致是( )
如图,一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是2m和αm(0<α<10),不考虑树的粗细,现用12m长的篱笆,借助墙角围成一个矩形花圃ABCD,设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位:m2)的图象大致是( )



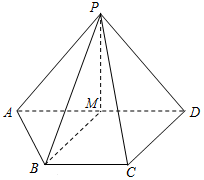 如图,在四棱锥P-ABCD中,M为AD的中点.
如图,在四棱锥P-ABCD中,M为AD的中点. 已知:三棱锥A-BCD中,平面ABD⊥平面BCD,AB⊥AD,E,F分别为BD,AD的中点.
已知:三棱锥A-BCD中,平面ABD⊥平面BCD,AB⊥AD,E,F分别为BD,AD的中点.