题目内容
已知
=(1，2)，
=(2x，-3)，且
∥
，则x=（ ）
| a |
| b |
| a |
| b |
| A、-3 | ||
| B、0 | ||
| C、x=16 | ||
D、x=-
|
考点：平行向量与共线向量,平面向量的坐标运算
专题：平面向量及应用
分析：直接利用向量共线的充要条件求解即可．
解答：
解：
=(1，2)，
=(2x，-3)，且
∥
，
∴-3=4x，
解得x=-
．
故选：D．
| a |
| b |
| a |
| b |
∴-3=4x，
解得x=-
| 3 |
| 4 |
故选：D．
点评：本题考查向量共线的充要条件的应用，基本知识的考查．
练习册系列答案
相关题目
设
、
为非零向量，已知命题p：若|
|=2sin
，|
|=4cos
，
•
=1，则
与
的和
；命题q：若函数f（x）=（x
+
）（
-x
）的图象关于y轴对称，则
=
．下列命题正确的是（ ）
| a |
| b |
| a |
| π |
| 24 |
| b |
| π |
| 24 |
| a |
| b |
| a |
| b |
| π |
| 12 |
| a |
| b |
| a |
| b |
| a |
| b |
| A、p∧q |
| B、p∧（￢q） |
| C、（￢p）∧q |
| D、（￢p）∧（￢q） |
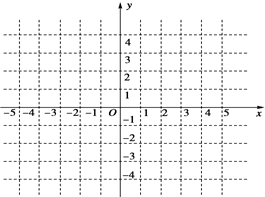设函数f（x）=x2-2|x|-3．
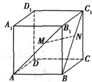如图，在正方体ABCD-A1B1C1D1中，M、N分别是对角线AB1、BC1上的点，且