题目内容
3.已知sinα=2cosα,计算:(1)$\frac{2sinα-cosα}{sinα+2cosα}$;
(2)sin2α+sinαcosα-2cos2α
分析 (1)由已知利用同角三角函数的基本关系求得,tanα=2,可得$\frac{2sinα-cosα}{sinα+2cosα}$=$\frac{2tanα-1}{tanα+2}$的值.
(2)根据sin2α+sinαcosα-2cos2α=$\frac{{{{sin}^2}α+sinαcosα-2{{cos}^2}α}}{{{{sin}^2}α+{{cos}^2}α}}$=$\frac{{tan}^{2}α+tanα-2}{{tan}^{2}α+1}$的值.
解答 解:(1)由已知得,tanα=2,
∴$\frac{2sinα-cosα}{sinα+2cosα}$=$\frac{2tanα-1}{tanα+2}$=$\frac{2×2-1}{2+2}=\frac{3}{4}$.
(2)sin2α+sinαcosα-2cos2α=$\frac{{{{sin}^2}α+sinαcosα-2{{cos}^2}α}}{1}$
=$\frac{{{{sin}^2}α+sinαcosα-2{{cos}^2}α}}{{{{sin}^2}α+{{cos}^2}α}}$=$\frac{{{{tan}^2}α+tanα-2}}{{{{tan}^2}α+1}}=\frac{4+2-2}{4+1}=\frac{4}{5}$.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
相关题目
18.给出下列两个命题:
命题:p:若在边长为1的正方形ABCD内任取一点M,则|MA|≤1的概率为$\frac{π}{4}$
命题:q:若函数f(x)=x+$\frac{4}{x}$,则f(x)在区间[1,$\frac{3}{2}$]上的最小值为4.
那么,下列命题为真命题的( )
命题:p:若在边长为1的正方形ABCD内任取一点M,则|MA|≤1的概率为$\frac{π}{4}$
命题:q:若函数f(x)=x+$\frac{4}{x}$,则f(x)在区间[1,$\frac{3}{2}$]上的最小值为4.
那么,下列命题为真命题的( )
| A. | p∧q | B. | ¬p | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
15.由0,1,2,3,5组成的无重复数字的五位偶数共有( )
| A. | 36个 | B. | 42个 | C. | 48个 | D. | 120个 |
17.已知函数f(log2x)的定义域为[1,4],则f(x)的定义域为( )
| A. | [2,16] | B. | [1,2] | C. | [0,8] | D. | [0,2] |
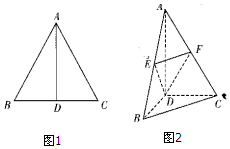 如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.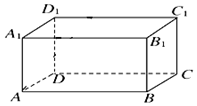 如图,长方体ABCD-A1B1C1D1中,AB=20,BC=13,AA1=12,过点A1D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形.
如图,长方体ABCD-A1B1C1D1中,AB=20,BC=13,AA1=12,过点A1D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形. 京剧是我国的国粹,是“国家级非物质文化遗产”,某机构在网络上调查发现各地京剧票友的年龄ξ服从正态分布N(μ,σ2),同时随机抽取100位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分别区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.
京剧是我国的国粹,是“国家级非物质文化遗产”,某机构在网络上调查发现各地京剧票友的年龄ξ服从正态分布N(μ,σ2),同时随机抽取100位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分别区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.