题目内容
三个数a=0.43,b=log30.4,c=30.4的大小关系是 (由大到小排列)
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用指数函数和对数函数的单调性求解.
解答:
解:∵0<a=0.43<0.40=1,
b=log30.4<log31=0,
c=30.4>30=1,
∴c>a>b.
故答案为:c>a>b.
b=log30.4<log31=0,
c=30.4>30=1,
∴c>a>b.
故答案为:c>a>b.
点评:本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意指数函数和对数函数的单调性的合理运用.

练习册系列答案
相关题目
已知向量
•
=0,|
|=|
|=1,且|
-
-2
|=1,则|
|的最大值( )
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
如图是一个几何体的三视图,则该几何体的体积是( )


| A、32+8π |
| B、16+8π |
| C、32+4π |
| D、16+4π |
已知函数f(x)=3x+x,g(x)=x+log3x,h(x)=log3x-
的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是( )
| 3 | x |
| A、x1>x2>x3 |
| B、x2>x1>x3 |
| C、x1>x3>x2 |
| D、x3>x2>x1 |
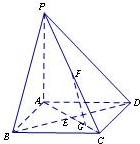 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.