题目内容
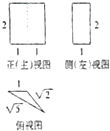
如图是一个几何体的三视图，则该几何体的体积是（ ）
| A、32+8π |
| B、16+8π |
| C、32+4π |
| D、16+4π |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三棱柱的三视图可得该几何体是一个长方体和圆柱的组合体，分别求出两个几何体的体积，相加可得答案．
解答：
解：由三棱柱的三视图可得该几何体是一个长方体和圆柱的组合体，
长方体的长宽高分别为：4，4，2，故体积为：4×4×2=32，
圆柱的底面直径为4，即底面半径为2，高为2，故体积为：π•22•2=8π，
故组合体的体积V=32+8π，
故选：A
长方体的长宽高分别为：4，4，2，故体积为：4×4×2=32，
圆柱的底面直径为4，即底面半径为2，高为2，故体积为：π•22•2=8π，
故组合体的体积V=32+8π，
故选：A
点评：本题考查了由三视图求原几何体的体积和表面积，解答的关键是由三视图还原原图形，是基础的计算题．
练习册系列答案
相关题目
已知一个三棱柱的三视图如图所示，则该三棱柱的表面积为（ ）
A、4
| ||||||
B、2
| ||||||
C、
| ||||||
D、2
|
设函数f（x）=
，g（x）=x2f（x-1），则函数g（x）的递减区间是（ ）
|
| A、（0，1] |
| B、（0，1） |
| C、（-∞，0） |
| D、（0，+∞） |