题目内容
10.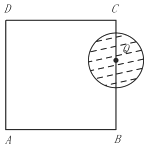 如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数),则m+n的取值范围是( )
如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数),则m+n的取值范围是( )| A. | $[{1-\frac{{\sqrt{2}}}{4},2+\frac{{\sqrt{2}}}{4}}]$ | B. | $[{\frac{3}{4},2+\frac{{\sqrt{2}}}{4}}]$ | C. | $[{\frac{3}{4},\frac{9}{4}}]$ | D. | $[{1-\frac{{\sqrt{2}}}{4},\frac{9}{4}}]$ |
分析 如图所示,$\overrightarrow{AB}$=( 4,0),$\overrightarrow{AD}$=(0,4).可得 $\overrightarrow{AP}$=m $\overrightarrow{AB}$+n $\overrightarrow{AD}$=( 4m,4n).当圆心为点B时,AP与⊙B相切且点P在x轴的下方时,P( 4-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
此时m+n取得最小值;当圆心为点C时,AP经过圆心时,P( $4+\frac{\sqrt{2}}{2}$,$4+\frac{\sqrt{2}}{2}$).此时m+n取得最大值.
解答 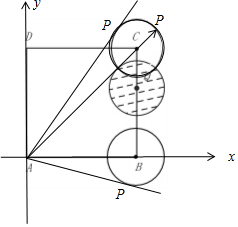 解:如图所示,边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数); $\overrightarrow{AB}$=( 4,0),$\overrightarrow{AD}$=(0,4).可得 $\overrightarrow{AP}$=m $\overrightarrow{AB}$+n $\overrightarrow{AD}$=( 4m,4n).
解:如图所示,边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数); $\overrightarrow{AB}$=( 4,0),$\overrightarrow{AD}$=(0,4).可得 $\overrightarrow{AP}$=m $\overrightarrow{AB}$+n $\overrightarrow{AD}$=( 4m,4n).
当动圆Q的圆心经过点C时,如图:P( $4+\frac{\sqrt{2}}{2}$,$4+\frac{\sqrt{2}}{2}$).
此时m+n取得最大值:4m+4n=8+$\sqrt{2}$,可得m+n=2+$\frac{\sqrt{2}}{4}$.
当动圆Q的圆心为点B时,AP与⊙B相切且点P在x轴的下方时,$\overrightarrow{AP}=(4+cosθ,sinθ)$,
此时,4m+4n=4-$\sqrt{2}$sin($θ+\frac{π}{4}$),
m+n取得最小值为:1-$\frac{\sqrt{2}}{4}$;此时P( 4-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
∴则m+n的取值范围为$[{1-\frac{{\sqrt{2}}}{4},2+\frac{{\sqrt{2}}}{4}}]$.
故选:A.
点评 本题考查了向量的坐标运算、点与圆的位置关系,考查了分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

 金钥匙试卷系列答案
金钥匙试卷系列答案| A. | {x|-2≤x<3} | B. | {x|0<x≤2} | C. | {x|-2≤x<0} | D. | {x|2≤x<3} |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |