题目内容
15．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右顶点分别为A、B，上顶点为C，若△ABC是底角为30°的等腰三角形，则$\frac{c}{a}$=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{6}}{3}$ |
分析 利用已知条件列出a，b关系式，最后求解离心率即可．
解答 解：由题意得∠CAB=30°，则tan∠CAB=$\frac{b}{a}$=$\frac{\sqrt{3}}{3}$，可得离心率为e=$\frac{c}{a}$=$\sqrt{\frac{{a}^{2}-{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{6}}{3}$，
故选：D．
点评 本题考查椭圆的简单性质的应用，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
10．
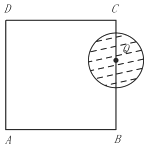如图，在边长为4的长方形ABCD中，动圆Q的半径为1，圆心Q在线段BC（含端点）上运动，P是圆Q上及内部的动点，设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$（m，n为实数），则m+n的取值范围是（ ）
如图，在边长为4的长方形ABCD中，动圆Q的半径为1，圆心Q在线段BC（含端点）上运动，P是圆Q上及内部的动点，设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$（m，n为实数），则m+n的取值范围是（ ）| A． | $[{1-\frac{{\sqrt{2}}}{4}，2+\frac{{\sqrt{2}}}{4}}]$ | B． | $[{\frac{3}{4}，2+\frac{{\sqrt{2}}}{4}}]$ | C． | $[{\frac{3}{4}，\frac{9}{4}}]$ | D． | $[{1-\frac{{\sqrt{2}}}{4}，\frac{9}{4}}]$ |
7．记min{a，b，c}为a，b，c中的最小值，若x，y为任意正实数，则M=min{2x，$\frac{1}{y}$，y+$\frac{1}{x}$}的最大值为（ ）
| A． | 1+$\sqrt{2}$ | B． | 2 | C． | 2+$\sqrt{2}$ | D． | $\sqrt{3}$ |
4．直线x-y+m=0与圆x2+y2-2x-1=0有两个不同交点的一个必要不充分条件是（ ）
| A． | 0＜m＜1 | B． | -4＜m＜0 | C． | m＜1 | D． | -3＜m＜1 |
如图所示：湖面上甲、乙、丙三艘船沿着同一条直线航行，某一时刻，甲船在最前面的A点处，乙船在中间B点处，丙船在最后面的C点处，且BC：AB=3：1．一架无人机在空中的P点处对它们进行数据测量，在同一时刻测得∠APB=30°，∠BPC=90°．（船只与无人机的大小及其它因素忽略不计）