题目内容
14．设集合A={x|x2-3x＜0}，B={x|x＞2}，则A∩∁RB=（ ）| A． | {x|-2≤x＜3} | B． | {x|0＜x≤2} | C． | {x|-2≤x＜0} | D． | {x|2≤x＜3} |
分析 先分别求出集合A，B，从而得到CRB，由此能求出A∩∁RB．
解答 解：∵集合A={x|x2-3x＜0}={x|0＜x＜3}，B={x|x＞2}，
∴CRB={x|x≤2}，
A∩∁RB={x|0＜x≤2}．
故选：B．
点评 本题考查补集、交集的求法，考查推理论证能力、运算求解能力，考查转化化归思想，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
4．已知直线x-y+1=0与双曲线$\frac{{x}^{2}}{a}$+$\frac{{y}^{2}}{b}$=1（ab＜0）相交于P，Q两点，且OP⊥OQ（O为坐标原点），则$\frac{1}{a}+\frac{1}{b}$=（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | $\sqrt{5}$ |
3．若sin（α+β）=2sin（α-β）=$\frac{1}{2}$，则sinαcosβ的值为（ ）
| A． | $\frac{3}{8}$ | B． | $-\frac{3}{8}$ | C． | $\frac{1}{8}$ | D． | $-\frac{1}{8}$ |
10．
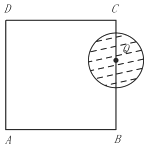如图，在边长为4的长方形ABCD中，动圆Q的半径为1，圆心Q在线段BC（含端点）上运动，P是圆Q上及内部的动点，设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$（m，n为实数），则m+n的取值范围是（ ）
如图，在边长为4的长方形ABCD中，动圆Q的半径为1，圆心Q在线段BC（含端点）上运动，P是圆Q上及内部的动点，设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$（m，n为实数），则m+n的取值范围是（ ）| A． | $[{1-\frac{{\sqrt{2}}}{4}，2+\frac{{\sqrt{2}}}{4}}]$ | B． | $[{\frac{3}{4}，2+\frac{{\sqrt{2}}}{4}}]$ | C． | $[{\frac{3}{4}，\frac{9}{4}}]$ | D． | $[{1-\frac{{\sqrt{2}}}{4}，\frac{9}{4}}]$ |