题目内容
12．已知直线l：mx+y-1+2m=0，则直线恒经过的定点（-2，1）．分析 直线mx+y+2m-1=0的方程可化为m（x+2）+（y-1）=0，根据x=-2，y=1时方程恒成立，可直线过定点的坐标．
解答 解：直线mx+y+2m-1=0的方程可化为：
m（x+2）+（y-1）=0，
当x=-2，y=1时方程恒成立
故直线mx+y+2m-1=0恒过定点（-2，1），
故答案为：（-2，1）．
点评 本题考查的知识点是恒过定义的直线，解答的关键是将参数分离，化为Am+B=0的形式（其中m为参数），令A，B=0可得答案．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
3．若sin（α+β）=2sin（α-β）=$\frac{1}{2}$，则sinαcosβ的值为（ ）
| A． | $\frac{3}{8}$ | B． | $-\frac{3}{8}$ | C． | $\frac{1}{8}$ | D． | $-\frac{1}{8}$ |
7．计算$\frac{1-i}{1+i}$（ ）
| A． | -1 | B． | i | C． | -i | D． | 1 |
10．
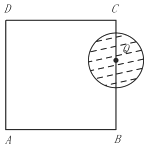如图，在边长为4的长方形ABCD中，动圆Q的半径为1，圆心Q在线段BC（含端点）上运动，P是圆Q上及内部的动点，设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$（m，n为实数），则m+n的取值范围是（ ）
如图，在边长为4的长方形ABCD中，动圆Q的半径为1，圆心Q在线段BC（含端点）上运动，P是圆Q上及内部的动点，设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$（m，n为实数），则m+n的取值范围是（ ）| A． | $[{1-\frac{{\sqrt{2}}}{4}，2+\frac{{\sqrt{2}}}{4}}]$ | B． | $[{\frac{3}{4}，2+\frac{{\sqrt{2}}}{4}}]$ | C． | $[{\frac{3}{4}，\frac{9}{4}}]$ | D． | $[{1-\frac{{\sqrt{2}}}{4}，\frac{9}{4}}]$ |
7．记min{a，b，c}为a，b，c中的最小值，若x，y为任意正实数，则M=min{2x，$\frac{1}{y}$，y+$\frac{1}{x}$}的最大值为（ ）
| A． | 1+$\sqrt{2}$ | B． | 2 | C． | 2+$\sqrt{2}$ | D． | $\sqrt{3}$ |