题目内容
5.已知二次函数f(x)=x2-bx+c在x=1处取得最小值-1.(1)解不等式|f(x)|+|f(-x)|≥6|x|;
(2)若实数a满足|x-a|<1,求证:|f(x)-f(a)|<2|a|+3.
分析 (1)求函数的解析式,分类讨论解不等式|f(x)|+|f(-x)|≥6|x|;
(2)由题意可得,|f(x)-f(a)|=|x-a|•|x+a-2|<|x+a-2|.再根据|x+a-2|=|x-a+2a-2|≤|x-a|+|2a-2|,再利用条件以及绝对值不等式的性质证得结论.
解答 (1)解:由题意,b=2,$\frac{4c-{b}^{2}}{4}$=-1,∴c=0,
∴f(x)=x2-2x,
∴|f(x)|+|f(-x)|≥6|x|,即|x2-2x|+|x2+2x|≥6|x|,
∴x=0或|x-2|+|x+2|≥6,
x≤-2,不等式可化为-x+2-x-2≥6,∴x≤-3,∴x≤-3;
-2<x<2,不等式可化为-x+2+x+2≥6,不成立;
x≥2,不等式可化为x-2+x+2≥6,∴x≥3,∴x≥3,
综上所述,不等式的解集为{x|x≤-3或x≥3或x=0};
(2)证明:∵f(x)=x2-2x,∴|f(x)-f(a)|=|x2-2x-a2+2a|=|x-a|•|x+a-2|,
∵实数a满足|x-a|<1,∴|x-a|•|x+a-2|<|x+a-2|.
又|x+a-2|=|x-a+2a-2|≤|x-a|+|2a-2|<1+|2a-2|≤1+|2|a|+2=2|a|+3,
∴|f(x)-f(a)|<2|a|+3.
点评 本题主要考查二次函数的性质,考查不等式的解法,考查绝对值不等式的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.某程序框图如图所示,分别输入下列选项中的四个函数,则可以输出的函数是( )


| A. | f(x)=x2+1 | B. | f(x)=sinx | C. | f(x)=2x | D. | f(x)=log2|x| |
7.计算$\frac{1-i}{1+i}$( )
| A. | -1 | B. | i | C. | -i | D. | 1 |
10.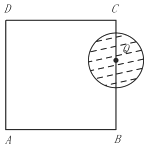 如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数),则m+n的取值范围是( )
如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数),则m+n的取值范围是( )
 如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数),则m+n的取值范围是( )
如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n为实数),则m+n的取值范围是( )| A. | $[{1-\frac{{\sqrt{2}}}{4},2+\frac{{\sqrt{2}}}{4}}]$ | B. | $[{\frac{3}{4},2+\frac{{\sqrt{2}}}{4}}]$ | C. | $[{\frac{3}{4},\frac{9}{4}}]$ | D. | $[{1-\frac{{\sqrt{2}}}{4},\frac{9}{4}}]$ |
17.点M为直线5x+12y=0上任一点,F1(-13,0),F2(13,0),则下列结论正确的是( )
| A. | ||MF1|-|MF2||>24 | B. | ||MF1|-|MF2||=24 | C. | ||MF1|-|MF2||<24 | D. | 以上都有可能 |
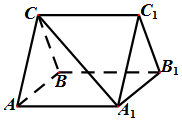 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.