题目内容
已知a＞0，b＞0，log9a=log12b=log162（a+b），则
= ．
| b |
| a |
考点：对数的运算性质
专题：函数的性质及应用
分析：设log9a=log12b=log162（a+b）=t，由指对互化求出a、b、2（a+b），求出
、列出2（9t+12t）=16t，两边同除以16t化简后利用换元法求出
，再由分母有理化求出
．
| a |
| b |
| a |
| b |
| b |
| a |
解答：
解：设log9a=log12b=log162（a+b）=t，
则a=9t，b=12t，2（a+b）=16t，即
=
=(
)t，
所以2（9t+12t）=16t，两边同除以16t可得，2(
)2t+2(
)t-1=0，
设(
)t=x（x＞0），代入上式得，2x2+2x-1=0，
解得x=
，
因为x＞0，所以x=
，
即
=(
)t=
，
=
=
+1，
故答案为：
+1．
则a=9t，b=12t，2（a+b）=16t，即
| a |
| b |
| 9t |
| 12t |
| 3 |
| 4 |
所以2（9t+12t）=16t，两边同除以16t可得，2(
| 3 |
| 4 |
| 3 |
| 4 |
设(
| 3 |
| 4 |
解得x=
-1±
| ||
| 2 |
因为x＞0，所以x=
-1+
| ||
| 2 |
即
| a |
| b |
| 3 |
| 4 |
-1+
| ||
| 2 |
| b |
| a |
| 2 | ||
|
| 3 |
故答案为：
| 3 |
点评：本题考查对数、指数的运算，指对互化，以及二次方程的实数根，考查换元法，分析、解决问题的能力．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
下列函数中，图象关于y轴对称的是（ ）
| A、y=log2x |
| B、y=x3 |
| C、y=cosx |
| D、y=sinx |
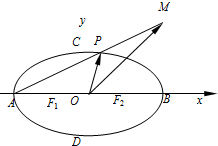如图，在直角坐标系xOy中，椭圆
如图，已知圆G：x2-x+y2=0，经过抛物线y2=2px的焦点，过点（m，0）（m＜0）倾斜角为
如图所示，在直三棱柱ABC-A1B1C1中，AC=4，BC=2，AB=2AA1=2