题目内容
7.下列命题中的真命题的序号为⑤.①函数y=$\frac{1}{x}$的单调递减区间是(-∞,0)∪(0,+∞).
②当n>0时,幂函数y=xn是定义域上的增函数.
③函数y=ax2+1(a>1)的值域是(0,+∞).
④log2x2=2log2x.
⑤若函数y=f(x)满足f(1+x)=f(1-x),则函数f(x)的图象关于直线x=1对称.
分析 ①,函数y=$\frac{1}{x}$的单调递减区间是(-∞,0),(0,+∞).
②,当n>0时,幂函数y=xn是(0,+∞)上的增函数.
③,函数y=ax2+1(a>1)的值域是[1,+∞).
④,当x>0,时,log2x2=2log2x才成立
⑤,根据轴对称的特征判定.
解答 解:对于①,函数y=$\frac{1}{x}$的单调递减区间是(-∞,0),(0,+∞),故错.
对于②,当n>0时,幂函数y=xn是(0,+∞)上的增函数,故错.
对于③,函数y=ax2+1(a>1)的值域是[1,+∞),故错.
对于④,当x>0,时,log2x2=2log2x才成立.故错
对于⑤,若函数y=f(x)满足f(1+x)=f(1-x),则函数f(x)的图象关于直线x=1对称.正确.
故答案为:⑤
点评 本题考查了命题真假的判定,涉及到了函数的概念及性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.若命题“p∨q”为真,且“¬p”为真,则( )
| A. | p或q为假 | B. | q假 | C. | q真 | D. | 不能判断q的真假 |
15.对具有线性相关的变量x,y有一组观测数据(xi,yi)(i=1,2,…6),其回归直线方程是$\widehaty=\frac{1}{4}x+a$,且x1+x2+…+x6=10,y1+y2+…+y6=4,则实数a的值是( )
| A. | $\frac{2}{3}$3 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
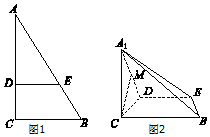 如图1,在Rt△ABC中,∠C=90°,BC=6,AC=9,D,E分别为AC、AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=6,AC=9,D,E分别为AC、AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.