题目内容
17.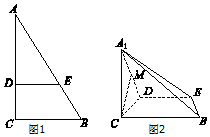 如图1,在Rt△ABC中,∠C=90°,BC=6,AC=9,D,E分别为AC、AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=6,AC=9,D,E分别为AC、AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.(1)求证:A1C⊥平面BCDE;
(2)若M是A1D的中点,求CM与平面A1BE所成角的正弦值.
分析 (1)推导出DE⊥AC,DE⊥A1D,DE⊥CD,从而DE⊥A1C.再由A1C⊥CD,能证明A1C⊥平面BCDE.
(2)以C为原点,CB为x轴,CD为y轴,CA1为z轴,建立空间直角坐标系,由此能求出CM与平面A1BE所成角的正弦值.
解答 证明:(1)∵AC⊥BC,DE∥BC,∴DE⊥AC.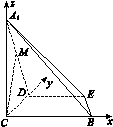
∴DE⊥A1C.
又∵A1C⊥CD,
∴A1C⊥平面BCDE.
解:(2)以C为原点,CB为x轴,CD为y轴,CA1为z轴,建立空间直角坐标系,
C(0,0,0),A1(0,0,3$\sqrt{3}$),D(0,3,0),M(0,$\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$),B(6,0,0),E(4,3,0),
$\overrightarrow{CM}$=(0,$\frac{3}{2},\frac{3\sqrt{3}}{2}$),$\overrightarrow{B{A}_{1}}$=(-6,0,3$\sqrt{3}$),$\overrightarrow{BE}$=(-2,3,0),
设平面A1BE的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{B{A}_{1}}=-6x+3\sqrt{3}z=0}\\{\overrightarrow{n}•\overrightarrow{BE}=-2x+3y=0}\end{array}\right.$,取x=1,$\overrightarrow{n}$=(1,$\frac{2}{3}$,$\frac{2\sqrt{3}}{3}$),
设CM与平面A1BE所成角为θ,
sinθ=$\frac{|\overrightarrow{n}•\overrightarrow{CM}|}{|\overrightarrow{n}|•|\overrightarrow{CM}|}$=$\frac{4}{3•\frac{5}{3}}$=$\frac{4}{5}$.
∴CM与平面A1BE所成角的正弦值为$\frac{4}{5}$.
点评 本题考查线面垂直,考查线面角,考查面面垂直,既有传统方法,又有向量知识的运用,要加以体会.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分条件也不必要条件 |
| A. | a3>a2(a>0,且a≠1) | B. | 0.30.8>0.30.7 | C. | π-1>e-1 | D. | log34>log43 |