题目内容
10.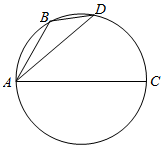 如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )| A. | 1 | B. | 2 | C. | t | D. | 2t |
分析 连结BC,CD,则$\overrightarrow{AB}•\overrightarrow{AC}$=AB2,$\overrightarrow{AD}•\overrightarrow{AC}$=AD2.于是$\overrightarrow{AC}$•$\overrightarrow{BD}$=$\overrightarrow{AC}•(\overrightarrow{AD}-\overrightarrow{AB})$=$\overrightarrow{AC}•\overrightarrow{AD}-\overrightarrow{AC}•\overrightarrow{AB}$.
解答 解:连结BC,CD.则AD⊥CD,AB⊥BC.
∴$\overrightarrow{AB}•\overrightarrow{AC}$=AB×AC×cos∠BAC=AB2=t+1.
$\overrightarrow{AD}•\overrightarrow{AC}$=AD×AC×cos∠CAD=AD2=t+2.
∵$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}$,
∴$\overrightarrow{AC}$•$\overrightarrow{BD}$=$\overrightarrow{AC}•(\overrightarrow{AD}-\overrightarrow{AB})$=$\overrightarrow{AC}•\overrightarrow{AD}-\overrightarrow{AC}•\overrightarrow{AB}$=1.
故选:A.
点评 本题考查了平面向量的数量积运算,使用圆周角定理计算向量的数量是解题关键.

| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
| A. | {x|x≥2} | B. | {x|x>-1} | C. | {x|x<2} | D. | {x|x<0} |