题目内容

19．在等差数列{an}中，若a1=25，S9=S17，则该数列的前（　　）项之和最大．
A．12B．13C．14D．15

分析 由求和公式代入已知易得公差，代入可得Sn的表达式，由二次函数性质可得答案．

解答 解：∵S9=S17，a1=25，设公差为d，由求和公式可得：
9×25+$\frac{9×（9-1）}{2}$d=17×25+$\frac{17（17-1）}{2}$d，
解得d=-2，
∴Sn=25n+$\frac{n（n-1）}{2}$（-2）=-（n-13）2+169．
由二次函数性质，可得前13项和最大．
故选：B．

点评 本题考查等差数列的求和公式，涉及二次函数的最值问题，属基础题．

练习册系列答案
相关题目
9．在△ABC中，若sinA+cosA=$\frac{7}{12}$，则这个三角形是（　　）
A．钝角三角形B．直角三角形C．锐角三角形D．等边三角形
10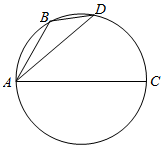．如图，B、D是以AC为直径的圆上的两点，其中AB=$\sqrt{t+1}$，AD=$\sqrt{t+2}$，则$\overrightarrow{AC}$•$\overrightarrow{BD}$=（　　）
A．1B．2C．tD．2t
7．已知一几何体的三视图如图所示，则该几何体的体积为（　　）
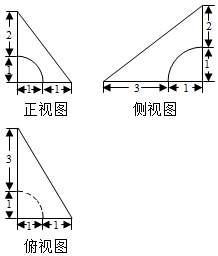
A．4$-\frac{π}{6}$B．4$-\frac{π}{3}$C．4$+\frac{π}{3}$D．12$-\frac{π}{6}$
14．函数y=3sinx-4cosx的最大值为5，最小值为-5．
5．设P是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$上一点，过椭圆中心作直线交椭圆于A、B两点，直线PA、PB的斜率分别为k1，k2，且${k_1}{k_2}=-\frac{1}{4}$，则椭圆离心率为$\frac{\sqrt{3}}{2}$．
12．设F是椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点，过F的直线与椭圆C交于A，B两点，分别过A，B作椭圆C的切线并相交于点P，线段OP（O为坐标原点）交椭圆C于点Q，满足$\overrightarrow{OQ}=2\overrightarrow{QP}$，且$\overrightarrow{FQ}•\overrightarrow{OF}=0$，则椭圆C的离心率为$\frac{\sqrt{6}}{3}$．
9．若函数f（x）=loga（x-1）+m（a＞0，且a≠1）恒过定点（n，2），则m+n的值为4．
10．已知定义在R上的奇函数f（x）满足f（x）=2x-4（x＞0），则{x|f（x-1）＞0}等于（　　）
A．{x|x＞3}B．{x|-1＜x＜1}C．{x|-1＜x＜1或x＞3}D．{x|x＜-1}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网