题目内容
1.在正项等比数列{an}中,a1a5-2a3a5+a3a7=36,a2a4+2a2a6+a4a6=100,求数列{an}的通项公式.分析 由已知式子可得a3和a5的值,分别可得q,可得通项公式.
解答 解:∵在正项等比数列{an}中a1a5-2a3a5+a3a7=36,a2a4+2a2a6+a4a6=100,
∴由等比数列的性质可得a32-2a3a5+a52=36,a32+2a3a5+a52=100,
∴(a3-a5)2=36,(a3+a5)2=100,
∴a3-a5=±6,a3+a5=10,
当a3-a5=6,a3+a5=10时,可解得a3=8,a5=2,
此时公比q=$\sqrt{\frac{{a}_{5}}{{a}_{3}}}$=$\frac{1}{2}$,an=8×($\frac{1}{2}$)n-3=($\frac{1}{2}$)n-6;
当a3-a5=-6,a3+a5=10时,可解得a3=2,a5=8;
此时公比q=$\sqrt{\frac{{a}_{5}}{{a}_{3}}}$=2,an=2×2n-3=2n-2;
点评 本题考查等比数列的通项公式,涉及方程组的解法和分类讨论思想,属基础题.

练习册系列答案
相关题目
11.已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为$\frac{4}{3}$的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )
| A. | $\frac{5}{7}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{7}}{7}$或$\frac{5}{7}$ | D. | $\frac{5}{7}$或$\frac{1}{3}$ |
9.在△ABC中,若sinA+cosA=$\frac{7}{12}$,则这个三角形是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 等边三角形 |
6.点D是△ABC中AB边的中点,CA=CB,E是CD的中点,AE的延长线交BC于F,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,则$\overrightarrow{AF}$=( )
| A. | $\frac{1}{4}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}\overrightarrow{b}$ |
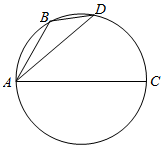 如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )