题目内容
1.设集合M={x|x≥2},集合N={x|x>-1},则 M∪N=( )| A. | {x|x≥2} | B. | {x|x>-1} | C. | {x|x<2} | D. | {x|x<0} |
分析 由M与N,求出两集合的并集即可.
解答 解:∵M={x|x≥2},N={x|x>-1},
∴M∪N={x|x>-1},
故选:B.
点评 此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
10.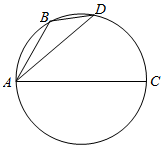 如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )
 如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )| A. | 1 | B. | 2 | C. | t | D. | 2t |
16.设全集U={1,2,3,4,5,6},集合M={1,4},N={1,3,5},则N∩(∁UM)=( )
| A. | {1} | B. | {3,5} | C. | {1,3,4,5} | D. | {1,2,3,5,6} |
6.F1,F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{2}$=1的左右焦点,P为椭圆上一动点,F2关于直线PF1的对称点为M,F1关于直线PF2的对称点为N,则当|MN|的最大值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | $2\sqrt{2}$ |
10.已知定义在R上的奇函数f(x)满足f(x)=2x-4(x>0),则{x|f(x-1)>0}等于( )
| A. | {x|x>3} | B. | {x|-1<x<1} | C. | {x|-1<x<1或x>3} | D. | {x|x<-1} |
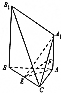 如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.
如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.