题目内容
15.设非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{c}$|,$\overrightarrow{a}$+$\overrightarrow{b}$=$\sqrt{3}$$\overrightarrow{c}$,则向量$\overrightarrow{a}$与向量$\overrightarrow{c}$的夹角为$\frac{π}{6}$.分析 作出图形,根据向量的几何意义和几何知识求出夹角.
解答  解:以$\overrightarrow{a},\overrightarrow{b}$为邻边作平行四边形OACB,∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,
解:以$\overrightarrow{a},\overrightarrow{b}$为邻边作平行四边形OACB,∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,
∴四边形OACB是菱形,$\overrightarrow{OC}=\overrightarrow{a}+\overrightarrow{b}$=$\sqrt{3}\overrightarrow{c}$.
设OA=AC=1,则OC=$\sqrt{3}$.
∴cos∠AOC=$\frac{1+3-1}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$.
∴∠AOC=$\frac{π}{6}$.
故答案为$\frac{π}{6}$.
点评 本题考查了平面向量加法的几何意义,向量的夹角计算,属于基础题.

练习册系列答案
相关题目
6.点D是△ABC中AB边的中点,CA=CB,E是CD的中点,AE的延长线交BC于F,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,则$\overrightarrow{AF}$=( )
| A. | $\frac{1}{4}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}\overrightarrow{b}$ |
10.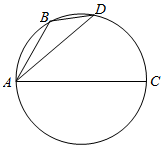 如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )
 如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中AB=$\sqrt{t+1}$,AD=$\sqrt{t+2}$,则$\overrightarrow{AC}$•$\overrightarrow{BD}$=( )| A. | 1 | B. | 2 | C. | t | D. | 2t |
7.已知一几何体的三视图如图所示,则该几何体的体积为( )
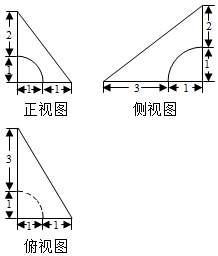

| A. | 4$-\frac{π}{6}$ | B. | 4$-\frac{π}{3}$ | C. | 4$+\frac{π}{3}$ | D. | 12$-\frac{π}{6}$ |