题目内容
A、B、C三点不共线,D为BC的中点,对于平面ABC内任意一点O都有
=2
-
-
,则( )
| OP |
| OA |
| 1 |
| 2 |
| OB |
| 1 |
| 2 |
| OC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:向量在几何中的应用
专题:平面向量及应用
分析:做出图形,根据向量的加法及减法的几何意义将
=2
-
-
进行化简为
=2
-
(
+
),然后通过作图将其表现出来,可看出四边形PODM是平行四边形,由此不难得到
=
.
| OP |
| OA |
| 1 |
| 2 |
| OB |
| 1 |
| 2 |
| OC |
| OP |
| OA |
| 1 |
| 2 |
| OB |
| OC |
| PA |
| AD |
解答:
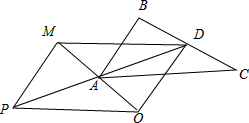
解:如图延长OA至M,使得OM=2OA,
又∵D是BD的中点,∴
+
=2
,
∴
=2
-
-
=2
-
(
+
)=
-
=
,
连接DA延长至P,使得DA=AP,
则四边形PODM是平行四边形,
∴
=
=2
-
-
,
由此可以得到
=
.
故选D
又∵D是BD的中点,∴
| OB |
| OC |
| OD |
∴
| OP |
| OA |
| 1 |
| 2 |
| OB |
| 1 |
| 2 |
| OC |
| OA |
| 1 |
| 2 |
| OB |
| OC |
| OM |
| OD |
| DM |
连接DA延长至P,使得DA=AP,
则四边形PODM是平行四边形,
∴
| OP |
| DM |
| OA |
| 1 |
| 2 |
| OB |
| 1 |
| 2 |
| OC |
由此可以得到
| PA |
| AD |
故选D

点评:利用向量解决几何问题,熟练掌握平面向量加法、减法、及数乘的几何意义是解题的关键.

练习册系列答案
相关题目
“x=2kπ+
(k∈Z)”是“|sinx|=1”的( )
| π |
| 2 |
| A、充分非必要条件 |
| B、必要分充分条件 |
| C、充要条件 |
| D、即非充分又非必要条件 |
函数y=sinx和y=cosx都是递减区间的是( )
A、[2kπ-
| ||
B、[2kπ-π,2kπ-
| ||
C、[2kπ+
| ||
D、[2kπ,2kπ+
|
不等式
>0的解集是( )
| x-2 |
| 1-x |
| A、{x|x>2或x<1} |
| B、{x|1<x<2} |
| C、{x|-1<x<2} |
| D、{x|x>2或x<-1} |
向如图中所示正方形内随机地投掷飞镖,飞镖落在阴影部分的概率为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
设抛物线C:y2=3px(p≥0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,3),则C的方程为( )
| A、y2=4x或y2=8x |
| B、y2=2x或y2=8x |
| C、y2=4x或y2=16x |
| D、y2=2x或y2=16x |
已知x与y之间的一组数据为
则y与x的回归直线方程
=
x+
必过定点( )
| x | 1 | 2 | 3 | 4 |
| y | 1 | 5-a | 3 | 7+a |
 |
| y |
 |
| b |
 |
| a |
A、(4,
| ||
B、(
| ||
| C、(6,8) | ||
D、(
|
若曲线f(x)=sinx+1在x=π处的切线与直线ax+2y+1=0相互垂直,则实数a等于( )
| A、2 | B、1 | C、-1 | D、-2 |