题目内容
设抛物线C:y2=3px(p≥0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,3),则C的方程为( )
| A、y2=4x或y2=8x |
| B、y2=2x或y2=8x |
| C、y2=4x或y2=16x |
| D、y2=2x或y2=16x |
考点:抛物线的简单性质,抛物线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:根据抛物线方程算出|OF|=
,设以MF为直径的圆过点A(0,2),在Rt△AOF中利用勾股定理算出|AF|=
.再由直线AO与以MF为直径的圆相切得到∠OAF=∠AMF,Rt△AMF中利用∠AMF的正弦建立关系式,从而得到关于p的方程,解之得到实数p的值,进而得到抛物线C的方程.
| 3p |
| 4 |
4+
|
解答:
解:∵抛物线C方程为y2=3px(p>0)
∴焦点F坐标为(
,0),可得|OF|=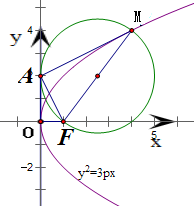
∵以MF为直径的圆过点(0,2),
∴设A(0,2),可得AF⊥AM
Rt△AOF中,|AF|=
∴sin∠OAF=
=
∵根据抛物线的定义,得直线AO切以MF为直径的圆于A点,
∴∠OAF=∠AMF,可得Rt△AMF中,sin∠AMF=
=
,
∵|MF|=5,|AF|=
∴
=
,整理得4+
=
,解之可得p=
或p=
因此,抛物线C的方程为y2=4x或y2=16x.
故选:C.
∴焦点F坐标为(
| 3p |
| 4 |

| 3p |
| 4 |
∵以MF为直径的圆过点(0,2),
∴设A(0,2),可得AF⊥AM
Rt△AOF中,|AF|=
4+
|
∴sin∠OAF=
| |OF| |
| |AF| |
| ||||
|
∵根据抛物线的定义,得直线AO切以MF为直径的圆于A点,
∴∠OAF=∠AMF,可得Rt△AMF中,sin∠AMF=
| |AF| |
| |MF| |
| ||||
|
∵|MF|=5,|AF|=
4+
|
∴
| ||||
| 5 |
| ||||
|
| 9p2 |
| 16 |
| 15p |
| 4 |
| 4 |
| 3 |
| 16 |
| 3 |
因此,抛物线C的方程为y2=4x或y2=16x.
故选:C.
点评:本题给出抛物线一条长度为5的焦半径MF,以MF为直径的圆交抛物线于点(0,2),求抛物线的方程,着重考查了抛物线的定义与简单几何性质、圆的性质和解直角三角形等知识,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
既在区间(0,
)上是增函数又是以π为周期的偶函数的是( )
| π |
| 2 |
| A、y=|cosx| |
| B、y=sin|x| |
| C、y=cos2x |
| D、y=|sinx| |
采用系统抽样方法从学号为1到50的50名学生中选取5名参加测试,则所选5名学生的学号可能是( )
| A、1,2,3,4,5 |
| B、5,26,27,38,49 |
| C、2,4,6,8,10 |
| D、5,15,25,35,45 |
已知函数f(x)=
,则不等式f(a2-4)>f(3a)的解集为( )
|
| A、(2,6) |
| B、(-1,4) |
| C、(1,4) |
| D、(-3,5) |
A、B、C三点不共线,D为BC的中点,对于平面ABC内任意一点O都有
=2
-
-
,则( )
| OP |
| OA |
| 1 |
| 2 |
| OB |
| 1 |
| 2 |
| OC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若(x+
)n展开式中第32项与第72项的系数相同,那么展开式的最中间一项的系数为( )
| 1 |
| x |
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
如图,D、E、F分别是边AB、BC、CA上的中点,则
+
-
=( )

| DE |
| DA |
| BE |

A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数中,是奇函数的是( )
| A、y=xcosx |
| B、y=sin|x| |
| C、y=sinx+1 |
| D、y=|sinx| |