题目内容
6.已知函数f(x)=2sin2($\frac{π}{4}$+x)-$\sqrt{3}$cos2x.(1)求f(x)的对称中心;
(2)若关于x的方程f(x)-m=2在x∈[$\frac{π}{4}$,$\frac{π}{2}$]上有二解,求实数m的取值范围.
分析 (1)先根据诱导公式以及二倍角公式,辅助角公式对函数化简,再结合正弦函数的图象和性质即可得到结论.
(2)先根据正弦函数的单调性求出f(x)的值域,再把方程有解转化为f(x)与m+2的取值范围相同即可求实数m的取值范围.
解答 (本题满分为12分)
解:(1)∵f(x)=2sin2($\frac{π}{4}$+x)-$\sqrt{3}$cos2x
=1-cos($\frac{π}{2}$+2x)-$\sqrt{3}$cos2x
=1+sin2x-$\sqrt{3}$cos2x
=2sin(2x-$\frac{π}{3}$)+1,…(4分)
∴由2x-$\frac{π}{3}$=kπ,k∈Z,解得:x=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,可得f(x)的对称中心为:($\frac{kπ}{2}$+$\frac{π}{6}$,1),k∈Z…(6分)
(2)∵x∈[$\frac{π}{4}$,$\frac{π}{2}$],所以2x-$\frac{π}{3}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],
∴sin(2x-$\frac{π}{3}$)∈[$\frac{1}{2}$,1],
所以f(x)的值域为[2,3],…(8分)
而f(x)=m+2,所以m+2∈[2,3],即m∈[0,1].(12分)
点评 本题主要考查三角函数中恒等变换应用以及整体代入思想的应用,在求三角函数的单调性时,一般都用整体代入思想,比如本题中令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,还考查了三角函数的对称中心的求解,要求熟练掌握正弦函数的图象和性质,属于中档题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
16.将向量$\overrightarrow{a_1}$=(x1,y1),$\overrightarrow{a_2}$=(x2,y2),…$\overrightarrow{a_n}$=(xn,yn)组成的系列称为向量列{$\overrightarrow{a_n}$},并定义向量列{$\overrightarrow{a_n}$}的前n项和$\overrightarrow{S_n}=\overrightarrow{a_1}+\overrightarrow{a_2}+…+\overrightarrow{a_n}$.如果一个向量列从第二项起,每一项与前一项的差都等于同一个向量,那么称这样的向量列为等差向量列.若向量列{$\overrightarrow{a_n}$}是等差向量列,那么下述四个向量中,与$\overrightarrow{{S_{21}}}$一定平行的向量是( )
| A. | $\overrightarrow{{a_{10}}}$ | B. | $\overrightarrow{{a_{11}}}$ | C. | $\overrightarrow{{a_{20}}}$ | D. | $\overrightarrow{{a_{21}}}$ |
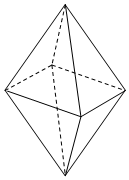 已知四面体的6条棱所在的直线中有3对异面直线,那么在过正八面体(由2个棱长相同的四棱锥拼接而成,如图所示)的任意2个顶点的所有直线中,随机取2条,则这2条直线异面的情况有24种.
已知四面体的6条棱所在的直线中有3对异面直线,那么在过正八面体(由2个棱长相同的四棱锥拼接而成,如图所示)的任意2个顶点的所有直线中,随机取2条,则这2条直线异面的情况有24种.