题目内容
15.为了测量学校操场四边形ABCD的周长和面积,在操场中间取一点O.测得OA=40m,OB=37m,OC=42m,OD=44m,且∠DOA=120°,∠AOB=60°,∠BOC=45°,∠COD=135°.(1)试求四边形的周长;
(2)试求四边形的面积.
分析 (1)使用余弦定理求出操场的边长;
(2)分别求出4个小三角形的面积.
解答 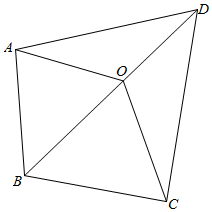 解:(1)在△AOB中,由余弦定理得:
解:(1)在△AOB中,由余弦定理得:
AB2=OA2+OB2-2OA•OBcos∠AOB=1489,∴AB≈38.6m.
同理可得BC2=OB2+OC2-2OB•OCcos∠BOC=935.3,∴BC≈30.9m
CD2=OD2+OC2-2OD•OCcos∠DOC=6313.47,∴BC≈79.5m
AD2=OA2+OD2-2OA•ODcos∠AOD=5296,∴BC≈72.77m
∴AB+BC+CD+AD=38.6+30.9+79.5+72.77=221.4m
即四边形的周长为221.4m.
(2)S△AOB=$\frac{1}{2}OA×OBsin∠AOB$=370$\sqrt{3}$,
S△BOC=$\frac{1}{2}OB×OC×sin∠BOC$=$\frac{777\sqrt{2}}{2}$,
S△COD=$\frac{1}{2}×OC×OD×sin∠COD$=462$\sqrt{2}$,
S△AOD=$\frac{1}{2}×OA×OD×sin∠AOD$=440$\sqrt{3}$.
∴四边形的面积S=S△AOB+S△BOC+S△COD+S△AOD=810$\sqrt{3}$+$\frac{1701\sqrt{2}}{2}$.
点评 本题考查了余弦定理的应用,三角形的面积公式,属于中档题.

练习册系列答案
相关题目
5.已知变量x、y满足的不等式组$\left\{\begin{array}{l}x≥0\\ 2x-y≤0\\ kx-y+1≥0\end{array}\right.$表示的平面区域是一个直角三角形,则实数k=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | 0或-$\frac{1}{2}$ |
20.已知角α是第二象限角,且$sinα=\frac{5}{13}$,则cosα=( )
| A. | -$\frac{12}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
 如图,在四边形ABCD中,BC=1,DC=2,四个内角A,B,C,D的度数之比为3:7:4:10.求:
如图,在四边形ABCD中,BC=1,DC=2,四个内角A,B,C,D的度数之比为3:7:4:10.求: