题目内容
若角α的终边经过点P(1,-2),则sinα=( )
A、
| ||||
B、-
| ||||
| C、-2 | ||||
D、-
|
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:由角α的终边经过点P(1,-2),利用任意角的三角函数定义求出sinα即可.
解答:
解:∵点P(1,-2),
∴x=1,y=-2,|OP|=
=
,
因此,sinα=
=
=-
.
故选:B.
∴x=1,y=-2,|OP|=
| 1+(-2)2 |
| 5 |
因此,sinα=
| y |
| |OP| |
| -2 | ||
|
2
| ||
| 5 |
故选:B.
点评:此题考查了同角三角函数间的基本关系,以及任意角的三角函数定义,熟练掌握三角函数的定义是解本题的关键.

练习册系列答案
相关题目
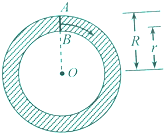 如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×
如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×| R+r |
| 2 |
| R+r |
| 2 |
| A、2πr2d |
| B、2π2r2d |
| C、2πrd2 |
| D、2π2rd2 |
复平面内与复数
对应的点所在的象限是( )
| 5i |
| 1-2i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
| ∫ | 2 0 |
| A、9 | B、11 | C、14 | D、18 |
已知i为虚数单位.z为复数,下面叙述正确的是( )
A、z-
| ||
| B、任何数的偶数次幂均为非负数 | ||
| C、i+1的共轭复数为i-l | ||
| D、2+3i的虚部为3 |
已知数列{an},a1=
,an=1-
(n≥2),则a2014=( )
| 1 |
| 4 |
| 1 |
| an-1 |
A、
| ||
B、
| ||
| C、-3 | ||
D、
|
 一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积V=
一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积V=