题目内容
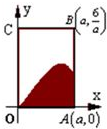如图，矩形OABC内阴影部分是由曲线f（x）=sinx（x∈（0，π）及直线x=a（a∈（0，π）与x轴围成，向矩形OABC内随机的投掷一点，若落在阴影部分的概率为| 1 |
| 4 |
考点：几何概型
专题：概率与统计
分析：利用积分求出阴影部分的面积，结合几何概型的概率公式，即可得到结论．
解答：
解：由题意可得，是与面积有关的几何概率．
构成试验的全部区域是矩形OACB，面积为：a×
=6，
记“向矩形OABC内随机投掷一点，若落在阴影部分”为事件A，
则构成事件 A的区域即为阴影部分面积为：S=
sinxdx=-cosx|0a=1-cosa，
由几何概率的计算公式可得P（A）=
=
，
得：cosa=-
，又a∈（0，π），
∴a=
，
故答案为：
．
构成试验的全部区域是矩形OACB，面积为：a×
| 6 |
| a |
记“向矩形OABC内随机投掷一点，若落在阴影部分”为事件A，
则构成事件 A的区域即为阴影部分面积为：S=
| ∫ | a 0 |
由几何概率的计算公式可得P（A）=
| 1-cosa |
| 6 |
| 1 |
| 4 |
得：cosa=-
| 1 |
| 2 |
∴a=
| 2π |
| 3 |
故答案为：
| 2π |
| 3 |
点评：本题是与面积有关的几何概率的计算，求解需要分别计算矩形的面积及阴影部分的面积，考查了利用积分计算不规则图象的面积．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
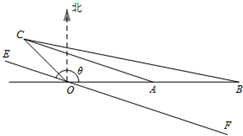如图，O为总信号源点，A，B，C是三个居民区，已知A，B都在O的正东方向上，OA=10km，OB=20km，C在O的北偏西45°方向上，CO=5
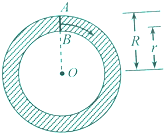如图，我们知道，圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形，又圆环的面积S=π（R2-r2）=（R-r）×2π×