题目内容
已知函数f(x)=Asin(ωx+
)(x∈R,A>0,ω>0)的最小正周期为T=6π,且f(2π)=2
(1)求ω和A的值;
(2)设α,β∈[0,
],f(3α+π)=
,f(3β+
)=-
;求cos(α-β)的值.
| π |
| 6 |
(1)求ω和A的值;
(2)设α,β∈[0,
| π |
| 2 |
| 16 |
| 5 |
| 5π |
| 2 |
| 20 |
| 13 |
考点:函数y=Asin(ωx+φ)的图象变换,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)通过函数的周期求出ω,利用f(2π)=2即可求出A的值;
(2)通过α,β∈[0,
],f(3α+π)=
,f(3β+
)=-
;分别求出cosα,cosβ,sinα,sinβ,然后利用两角和与差的三角函数直接求cos(α-β)的值.
(2)通过α,β∈[0,
| π |
| 2 |
| 16 |
| 5 |
| 5π |
| 2 |
| 20 |
| 13 |
解答:
解:(1)依题意得ω=
=
=
,
∴函数f(x)=Asin(
+
) (2分)
由f(2π)=2得Asin(
+
)=2,
即 Asin
=2,
∴A=4 (4分)
∴函数f(x)=4sin(
+
) (5分)
(2)由f(3α+π)=
,得4sin[
(3α+π)+
]=
,
即4sin(α+
)=
.
∴cosα=
,(6分)
又∵α∈[0,
],∴sinα=
.(7分)
由f(3β+
)=-
得4sin[
(3β+
)+
]=-
,即sin(β+π)=-
,
∴sinβ=
,(9分)
又∵β∈[0,
],
∴cosβ=
(10分)
cos(α-β)=cosαcosβ+sinαsinβ=
×
+
×
=
.(12分)
| 2π |
| T |
| 2π |
| 6π |
| 1 |
| 3 |
∴函数f(x)=Asin(
| x |
| 3 |
| π |
| 6 |
由f(2π)=2得Asin(
| 2π |
| 3 |
| π |
| 6 |
即 Asin
| 5π |
| 6 |
∴A=4 (4分)
∴函数f(x)=4sin(
| x |
| 3 |
| π |
| 6 |
(2)由f(3α+π)=
| 16 |
| 5 |
| 1 |
| 3 |
| π |
| 6 |
| 16 |
| 5 |
即4sin(α+
| π |
| 2 |
| 16 |
| 5 |
∴cosα=
| 4 |
| 5 |
又∵α∈[0,
| π |
| 2 |
| 3 |
| 5 |
由f(3β+
| 5π |
| 2 |
| 20 |
| 13 |
| 1 |
| 3 |
| 5π |
| 2 |
| π |
| 6 |
| 20 |
| 13 |
| 5 |
| 13 |
∴sinβ=
| 5 |
| 13 |
又∵β∈[0,
| π |
| 2 |
∴cosβ=
| 12 |
| 13 |
cos(α-β)=cosαcosβ+sinαsinβ=
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 63 |
| 65 |
点评:本题考查两角和与差的三角函数,函数的解析式的求法,考查计算能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
若向量
=(2,-1),
=(0,2),则以下向量中与
+
垂直的是( )
| a |
| b |
| a |
| b |
| A、(1,-2) |
| B、(1,2) |
| C、(2,1) |
| D、(0,2) |
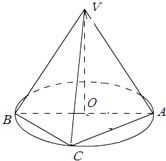 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,已知AB=2,VA=VB=VC=2.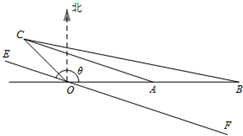 如图,O为总信号源点,A,B,C是三个居民区,已知A,B都在O的正东方向上,OA=10km,OB=20km,C在O的北偏西45°方向上,CO=5
如图,O为总信号源点,A,B,C是三个居民区,已知A,B都在O的正东方向上,OA=10km,OB=20km,C在O的北偏西45°方向上,CO=5