题目内容
4.在直角坐标系xOy中,曲线${C_1}:\left\{{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}}\right.$(t为参数,t≠0),其中0≤a<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4sinθ,曲线${C_3}=ρ=4\sqrt{3}cosθ$.(Ⅰ)求C2与C3交点的直角坐标系;
(Ⅱ)若C2与C1相交于点A,C3与C1相交于点B,求|AB|的最大值.
分析 (Ⅰ)通过极坐标方程与普通方程的转化公式,代入化简即可;
(Ⅱ)通过联立C2与C1、C3与C1可知A的极坐标为(4sinα,α)、B的极坐标为(4$\sqrt{3}$cosθ,α),进而利用辅助角公式,结合三角函数的有界性即得结论.
解答 解:(Ⅰ)因为C2:ρ=4sinθ,
所以ρ2=4ρsinθ,
故C2:x2+y2-4y=0;
因为C3:ρ=4$\sqrt{3}$cosθ,
所以ρ2=4$\sqrt{3}$ρcosθ,
故C3:${x}^{2}+{y}^{2}-4\sqrt{3}x=0$;
联立得交点坐标为(0,0),($\sqrt{3}$,3).
(Ⅱ)曲线C1的极坐标方程为θ=α(ρ∈R,ρ≠0),其中0≤α<π,
因此得到A的极坐标为(4sinα,α),B的极坐标为(4$\sqrt{3}$cosθ,α).
所以|AB|=|4$\sqrt{3}$cosθ-4sinθ|=|8cos($\frac{π}{6}$+α)|,
当α=$\frac{5π}{6}$时,|AB|取得最大值,最大值为8.
点评 本题考查极坐标与参数方程,考查运算求解能力,涉及辅助角公式,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
14.已知△ABC的顶点都在半径为R的球O的球面上,球心O到平面ABC的距离为$\frac{{\sqrt{3}}}{2}R$,$AB=BC=AC=\sqrt{3}$,则球O的体积是( )
| A. | $\frac{16}{3}π$ | B. | 16π | C. | $\frac{32}{3}π$ | D. | 32π |
19.设复数z1和z2关于虚轴对称且z1=2+i,那么z1z2等于( )
| A. | -5 | B. | 5 | C. | -4 | D. | 4 |
9.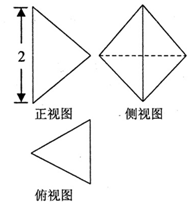 某几何体的三视图如图所示,其俯视图是边长为1的正三角形,侧视图是菱形,则这个几何体的体积为( )
某几何体的三视图如图所示,其俯视图是边长为1的正三角形,侧视图是菱形,则这个几何体的体积为( )
 某几何体的三视图如图所示,其俯视图是边长为1的正三角形,侧视图是菱形,则这个几何体的体积为( )
某几何体的三视图如图所示,其俯视图是边长为1的正三角形,侧视图是菱形,则这个几何体的体积为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |