题目内容
1.设f(x)=$\frac{mx}{1+|x|}$,集合N={y|y=f(x),x∈[a,b]},若使得N=[a,b]的实数对(a,b)(a<b)恰好有3个,则实数m的取值范围是m>1.分析 由题意判断函数f(x)=$\frac{mx}{1+|x|}$的奇偶性与单调性,从而转化为函数的图象的交点的个数问题,从而结合图象解得.
解答 解:令y=$\frac{x}{1+|x|}$,
易知y=$\frac{x}{1+|x|}$在R上是奇函数且单调递增,
当m<0时,
f(x)=$\frac{mx}{1+|x|}$在R上是减函数且是奇函数,
若N={y|y=f(x),x∈[a,b]}=[a,b],
则f(a)=b,且f(b)=a,
由点(a,b)与点(b,a)关于y=x对称,
则a<0<b,
∴f(-a)=-f(a)=-b,
若b<-a,则f(b)>f(-a),a>-b,-a<b矛盾,
若b>-a,则f(b)<f(-a),a<-b,-a>b矛盾,
故b=-a,
故f(x)=-x的非零解,
即f(x)与直线y=-x的非零交点的个数,
结合图象可知,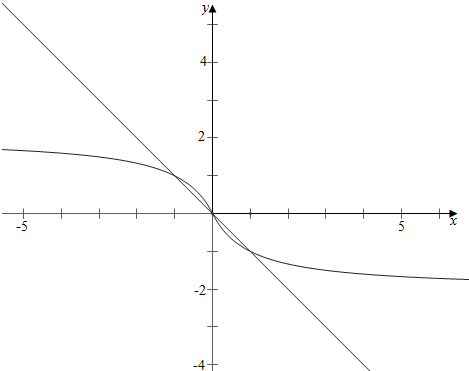 ,
,
最多有一对非零交点,故不成构成3对;
当m=0时,显然不成立;
当m>0时,同理可化为f(x)与直线y=x的交点的个数,
结合图象可知,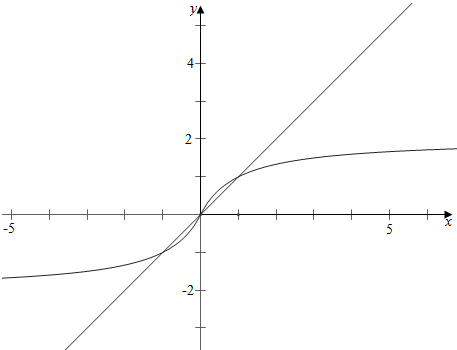
由方程$\frac{mx}{1+|x|}$=x知,
当m>1时,有三个交点,
可构成3对(a,b);
当0<m≤1时,不能构成3对(a,b);
故答案为:m>1.
点评 本题考查了函数的性质的判断与应用,同时考查了数形结合的思想应用.

练习册系列答案
相关题目
12.已知函数f(x)=|3x-1|,当a<b<c时,有f(a)>f(c)>f(b),则下列各式中正确的是( )
| A. | 3a+3b<2 | B. | 3b+3c<2 | C. | 3a+3c<2 | D. | 3a+3c<1 |
16.已知点A,B分别为异面直线a,b上的点,且直线AB与a,b均垂直,动点P∈a,Q∈b,PA+QB为定值,则线段PQ中点M的轨迹是( )
| A. | 平行四边形 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别F1(-c,0),F2(c,0),若双曲线上存在点P满足$\frac{a}{sin∠PF{{\;}_{1}F}_{2}}$=$\frac{c}{sin∠P{F}_{2}{F}_{1}}$1,则该曲线的离心率的取值范围为( )
| A. | (1,$\sqrt{2}$+1) | B. | (1,$\sqrt{3}$) | C. | ($\sqrt{3}$,+∞) | D. | ($\sqrt{2}$+1,+∞) |
13.已知命题p:x+y≠6,命题q:x≠2或y≠4,则命题p是命题q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.在用1,2,3,4,5这5个数组成的全部无重复数字的三位数中,能被3整除的有( )
| A. | 20个 | B. | 24个 | C. | 30个 | D. | 32个 |
11.“α是第二象限角“是“sinαcosα<0”的( )
| A. | 充分不必要条件 | B. | 不要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 函数y=Asin(ωx+φ)+k在一个周期内的图象如图所示,且ω>0,求其解析式.
函数y=Asin(ωx+φ)+k在一个周期内的图象如图所示,且ω>0,求其解析式.