题目内容
12.已知函数f(x)=|3x-1|,当a<b<c时,有f(a)>f(c)>f(b),则下列各式中正确的是( )| A. | 3a+3b<2 | B. | 3b+3c<2 | C. | 3a+3c<2 | D. | 3a+3c<1 |
分析 可以画出函数f(x)的图象,根据条件,通过图象就能找到a,b,c的分布情况,能判断这三个数在x=0的左面还是右面.从而找出正确的结论.
解答 解:函数f(x)=|3x-1|=$\left\{\begin{array}{l}-{3}^{x}+1,x<0\\{3}^{x}-1,x≥0\end{array}\right.$;
∴x<0时,函数是减函数;x≥0时,是增函数;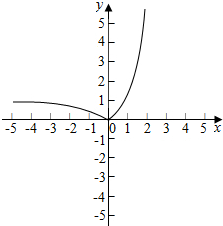
∵a<b<c,
∴若c≤0,则f(a)>f(b)>f(c),不合题意,
∴c>0;
若a≥0,则f(a)<f(b)<f(c),也不合题意,
∴a<0,而b可大于0,可小于0.
∴由f(a)>f(c)知,-3a+1>3c-1,
∴3a+3c<2.
故选:C.
点评 本题考查的知识点是分段函数的应用,能够画出函数f(x)的图象,或能判断函数f(x)的单调性,是解答的关键.

练习册系列答案
相关题目
3.已知P(3cosα,3sinα,1)和Q(2cosβ,2sinβ,1),则|$\overrightarrow{PQ}$|的取值范围是( )
| A. | (1,25) | B. | [1,25] | C. | [1,5] | D. | (1,5) |
20.若P是等边三角形ABC所在平面外一点,且PA=PB=PC,D,E,F分别是AB,BC,CA的中点,则下列结论中不正确的是( )
| A. | BC∥平面PDF | B. | DF⊥平面PAE | C. | 平面PAE⊥平面ABC | D. | 平面PDF⊥平面ABC |
17.命题“?x∈R,x2≥0”的否定是( )
| A. | ?x0∈R,x${\;}_{0}^{2}$<0 | B. | ?x∈R,x${\;}_{0}^{2}$≤0 | C. | ?x∈R,x2<0 | D. | ?x∈R,x2≤0 |
4.设实数数列{an}(n∈N*)是等差数列,且a12+a22=1,则a22+a32的取值范围是( )
| A. | [1,2] | B. | [4-2$\sqrt{3}$,4+2$\sqrt{3}$] | C. | [1,5] | D. | [3-2$\sqrt{2}$,3+2$\sqrt{2}$] |